Значения капитала и прибыли в среднем на один банк существенно различаются по группам:

· в первой группе капитал составляет 800,7 млн. руб., прибыль 15,7 млн. руб.;

· во второй группе значение капитала в среднем на один банк составляет 906 млн. руб., что в 1,13 раза выше, чем в первой группе, прибыль составляет 19,6 млн. руб., что в 1,25 раза выше, чем в первой группе;

· в третьей группе показатели в среднем на один банк капитала и прибыли составляют 987,5 млн. руб. и 23,6 млн. руб. соответственно, что по капиталу превосходит аналогичный показатель первой группы в 1,23 раза и второй группы в 1,09 раза, по прибыли превосходит аналогичный показатель первой группы в 1,5 раза, а второй группы в 1,2 раза.

Таким образом, сопоставление роста прибыли по группам и роста величины капитала, также свидетельствует о наибольшей эффективности банков третьей группы.

4. Проверка однородности и нормальности распределения

Необходимой предпосылкой корректного использования статистических методов анализа является однородность совокупности. Неоднородность совокупности возникает вследствие значительной вариации значений признака или попадания в совокупность резко выделяющихся, так называемых «аномальных» наблюдений. Для их выявления используем правило трех сигм, которое состоит в том, что «аномальными» будут те банки, у которых значения анализируемого признака будут выходить за пределы интервала, т.е.:

где		среднее значение факторного показателя
	среднее квадратическое отклонение по факторному показателю
	значение факторного показателя

Выделив и исключив «аномальные» банки, оценку однородности проведем по коэффициенту вариации, который должен быть не более 33,3%:

где		коэффициент вариации
	среднее значение факторного показателя
	среднее квадратическое отклонение по факторному показателю

Для выявления «аномальных» наблюдений по первичным данным о величине капитала вычислим его среднюю величину и среднее квадратическое отклонение (См. таблицу №4):

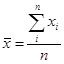
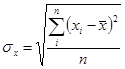
где		среднее значение факторного показателя
	среднее квадратическое отклонение по факторному показателю
	значение факторного показателя
	число единиц в совокупности

Таблица №4
№ банка п/п	Капитал, млн. руб.			Прибыль, млн. руб.
1	2	3	4	5	6	7	8
1	982	102	10 404	35,1	16,2	262,44	1 652,4
2	971	91	8 281	22,6	3,7	13,69	336,7
3	965	85	7 225	20,1	1,2	1,44	102,0
4	1045	165	27 225	20,8	1,9	3,61	313,5
5	1004	124	15 376	23,8	4,9	24,01	607,6
6	958	78	6 084	19,3	0,4	0,16	31,2
7	932	52	2 704	21,3	2,4	5,76	124,8
8	931	51	2 601	18,4	- 0,5	0,25	- 25,5
9	928	48	2 304	20,2	1,3	1,69	62,4
10	924	44	1 936	19,4	0,5	0,25	22,0
11	921	41	1 681	20,6	1,7	2,89	69,7
12	901	21	441	15,6	- 3,3	10,89	- 69,3
13	880	0	0	21,3	2,4	5,76	0,0
14	873	- 7	49	18,1	- 0,8	0,64	5,6
15	864	- 16	256	21,2	2,3	5,29	- 36,8
16	859	- 21	441	18,4	- 0,5	0,25	10,5
17	804	- 76	5 776	16,5	- 2,4	5,76	182,4
18	821	- 59	3 481	17,2	- 1,7	2,89	100,3
19	801	- 79	6 241	18,0	- 0,9	0,81	71,1
20	801	- 79	6 241	19,4	0,5	0,25	- 39,5
21	800	- 80	6 400	15,3	- 3,6	12,96	288,0
22	785	- 95	9 025	14,4	- 4,5	20,25	427,5
23	794	- 86	7 396	12,5	- 6,4	40,96	550,4
24	795	- 85	7 225	16,2	- 2,7	7,29	229,5
25	770	- 110	12 100	11,5	- 7,4	54,76	814,0
26	778	- 102	10 404	13,8	- 5,1	26,01	520,2
Итого:		22 887	161 297	491,0	510,96	6 350,7

Поскольку минимальное значение капитала (770 млн. руб.) больше нижней границы интервала (643 млн. руб.), а максимальное значение (1045 млн. руб.) меньше верхней границы (1117 млн. руб.), то можно считать, что в данной совокупности «аномальных» наблюдений нет.

Проверка однородности осуществляется по коэффициенту вариации:

Т.к. , следовательно, данная совокупность однородна.

5. Построение ряда распределения

Для построения ряда распределения необходимо определить число групп и величину интервала. Для определения числа групп воспользуемся формулой Стерджесса:

где		число групп (всегда целое)
	число единиц в совокупности

Величину интервала определим по формуле:

где		максимальное значение факторного признака
	минимальное значение факторного признака
	число групп

Нижнюю границу первого интервала принимаем равной минимальному значению факторного признака, а верхнюю границу каждого интервала получаем прибавлением к нижней границе величины интервала. По каждой группе подсчитываем число банков, за принимаем середину интервала, условно считая, что она будет равной средней по интервалу, и результаты заносим в таблицу №5:

Таблица №5
№ п/п	Капитал, млн. руб.	Число банков
1	2	3	4	5	6	7	8	9	10
I	770 – 825	10	797,5	7 975,0	10	- 78,5	785,0	6 162,25	61 622,50
II	825 – 880	3	852,5	2 557,5	13	- 23,5	70,5	552,25	1 656,75
III	880 – 935	7	907,5	6 352,5	20	31,5	220,5	992,25	6 945,75
IV	935 – 990	4	962,5	3 850,0	24	86,5	346,0	7 482,25	29 929,00
V	990 – 1045	2	1 017,5	2 035,0	26	141,5	283,0	20 022,25	40 044,50
Итого:		26	22 770	1 705,0	140 198,50

Среднюю по ряду распределения рассчитываем по средней арифметической взвешенной:

где		средняя по ряду распределения
	средняя по i -му интервалу
	частота i -го интервала (число банков в интервале)

Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:

где		значение моды
	нижняя граница модального интервала
	величина модального интервала
	частота модального интервала
	частота интервала, предшествующего модальному
	частота послемодального интервала

Модальный интервал определяется по наибольшей частоте. Для данного ряда наибольшее значение частоты равно 10, т.е. это будет интервал 770 – 825, тогда значение моды:

Медиана – значение признака, лежащее в середине ранжированного (упорядоченного) ряда распределения.

Номер медианы определяется по формуле:

где		номер медианы
	число единиц в совокупности

т.к. медианы с дробным номером не бывает, то полученный результат указывает, что медиана находится посередине между 13-й и 14-й величинами совокупности.

Значение медианы можно определить по формуле:

где		значение медианы
	нижняя граница медианного интервала
	величина медиального интервала
	номер медианы
	накопленная частота интервала, предшествующего медианному
	частота медианного интервала

По накопленной частоте определяем, что медиана будет находиться в интервале 880 – 935, тогда значение медианы: