Доверительный интервал для средней величины генеральной совокупности:

где		средняя величина факторного признака выборочной совокупности
	средняя величина факторного признака генеральной совокупности
	предельная ошибка средней величины факторного признака

Следовательно, с вероятностью 0,95 можно гарантировать, что средняя величина капитала в расчете на один банк по генеральной совокупности будет находиться в пределах от до

Средняя ошибка выборки доли банков, у которых капитал превышает среднюю величину, для бесповторного отбора:

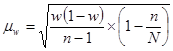
где		дисперсия доли банков выборочной совокупности
	численность единиц выборочной совокупности
	численность единиц генеральной совокупности

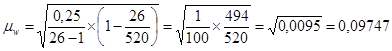
Предельная ошибка доли банков рассчитывается по формуле:

где		средняя ошибка выборки доли банков
	коэффициент доверия

Коэффициент доверия при вероятности по таблице Стьюдента уже был определен, и он составляет . Тогда, предельная ошибка доли:

Доверительный интервал для доли банков в генеральной совокупности:

где		доля банков по выборочной совокупности
	доля банков по генеральной совокупности
	предельная ошибка доли

Следовательно, с вероятностью 0,95 можно гарантировать, что доля банков, у которых величина капитала больше среднего значения, по генеральной совокупности будет находиться в пределах от до .

7. Установка наличия и характера связи

Связь между факторными и результативными показателями может быть одной из двух видов: функциональной или корреляционной.

Функциональной, называется такая взаимосвязь, которая проявляется с одинаковой силой у всех единиц совокупности, независимо от изменения других признаков данного явления. Функциональные связи обычно выражаются формулами.

Корреляционной называется взаимосвязь между факторным и результа­тив­ным показателем, которая проявляется только «в общем и среднем» при массовом наблюдении фактических данных.

Содержательный анализ исходных данных выполнен ранее и установлено, что капитал – факторный признак , прибыль – результативный , поэтому на основании проведенных ранее вычислений можно сделать однозначный вывод, что связь между факторным и результативным признаком не полная, а проявляется лишь в общем, среднем, т.е. речь может идти только о корреляционном виде связи.

Непременными условиями корректного использования корреляционного метода являются достаточно большое число единиц совокупности, однородность совокупности и отсутствие выделяющихся, «аномальных» наблюдений, проверка которых уже выполнена в п.4 данного задания.

Для установки факта наличия связи, заполним групповую таблицу №5а, по данным таблицы №5; на рисунке №1 построим поле корреляции, по исходным данным таблицы №1, и эмпирическую линию регрессии, по данным таблицы №5а, принимая середину интервала за , за – прибыль в среднем на один банк:

Таблица №5а
№ п/п	Капитал, млн. руб.	Число Банков	Середина интервала, млн. руб.	Прибыль в среднем на один банк, млн. руб.
1	2	3	4	5
I	770 – 825	10	797,5	15,48
II	825 – 880	3	852,5	19,23
III	880 – 935	7	907,5	19,54
IV	935 – 990	4	962,5	24,27
V	990 – 1045	2	1017,5	22,30

Анализ таблицы №5а свидетельствует, что существует зависимость между капиталом и прибылью банков.

???? ??????????, ????? ????? ?????????? ??????? ? ???? ??????????, ??? ??????? ????????? ? ????? ?? ?????? ??????? ???? ? ?????? ???????. ??????, ??????? ?????? ?????????????? ??????????? ????? ????????? ? ???????? ??????.

Эмпирическая линия регрессии также имеет некоторую тенденцию к росту, что также свидетельствует о наличии прямой корреляционной зависимости между капиталом и прибылью банков.

8. Определение тесноты и существенности связи

Эмпирическая линия регрессии (рисунок №1) – ломаная линия. Изломы этой линии свидетельствуют о влиянии на признак прочих факторов, помимо признака . Чтобы абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию полученной ломаной линии регрессии. Для этого сначала необходимо установить теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим образом отображающий характер изучаемой связи.

Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе, но этот выбор всегда связан с некоторой условностью, вызванный тем, что нужно находить форму функциональной зависимости, в то время как зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая, т.е. довольно близко приближается к функциональной, тогда именно теоретическая линия регрессии и ее параметры приобретают практическое значение.

На основании качественного анализа исходных данных (таблица №1) и эмпирической линии регрессии (рисунок №1) можно предположить, что между капиталом и прибылью банков существует линейная зависимость. Для определения тесноты этой зависимости воспользуемся линейным коэффициентом корреляции:

где		значение факторного показателя
	среднее значение факторного показателя
	значение результативного показателя
	среднее значение результативного показателя
	число единиц в совокупности
	среднее квадратическое отклонение по факторному показателю
	среднее квадратическое отклонение по результативному показателю

Для вычисления линейного коэффициента корреляции воспользуемся расчетами, выполненными в таблице №4, тогда