Наряду со средними величинами большое значение имеет изучение отклонений от средних, при этом представляет интерес совокупность всех отклонений, т.к. от их размера и распределения зависит типичность и надежность средних характеристик. Наиболее простым из этих показателей является показатель размаха вариации, который рассчитывается по формуле:

где		размах вариации
	максимальное значение признака
	минимальное значение признака

Размах вариации характеризует разброс только крайних значений, поэтому он не может быть достоверной характеристикой вариации признака. Распределение отклонений можно уловить, определив все отклонения от средней, для этого можно определить среднее арифметическое (линейное) отклонение, которое рассчиты­вается по формуле:

где		среднее линейное отклонение
	средняя по ряду распределения
	средняя по i -му интервалу
	частота i -го интервала (число банков в интервале)

Среднее линейное отклонение, как меру вариации признака применяют крайне редко. Чаще отклонения от средней возводят в квадрат и из квадратов отклонений вычисляют среднюю величину. Полученная мера вариации называется дисперсией, а корень квадратный из дисперсии, есть среднее квадратическое отклонение, которое выражает абсолютную меру вариации и вычисляется по формуле:

где		среднее квадратическое отклонение
	дисперсия
	средняя по ряду распределения
	средняя по i -му интервалу
	частота i -го интервала (число банков в интервале)

По рассчитанным показателям достаточно трудно судить о степени вариации признака в совокупности, т.к. их величина зависит от размера значений признака, поэтому более объективной характеристикой будет коэффициент вариации, который рассчитывается по формуле:

где		коэффициент вариации
	среднее квадратическое отклонение
	средняя по ряду распределения

Т.к. , следовательно, данное значение коэффициента вариации свидетельствует об однородности совокупности и надежности средней.

Для характеристики дифференциации банков по величине капитала, рассчитаем коэффициент фондовой дифференциации по формуле:

где		коэффициент фондовой дифференциации
	средняя из 10% максимальных значений признака
	средняя из 10% минимальных значений признака

Т.к. 10% от 26 будет 2,6, то можно взять значения трех банков, имеющих самые большие и самые меньшие значения капитала:

: 770; 778; 785

: 1045; 1004; 982

Тогда:

Следовательно, средняя из 10% максимальных значений в 1,3 раза превышает среднюю из 10% минимальных значений.

6. Определение характеристик генеральной совокупности

По условию задания предполагается, что исходные данные по 26 банкам являются 5% выборкой из некоторой генеральной совокупности. Для определения характеристик генеральной совокупности необходимо:

· определить характеристики выборочной совокупности: среднюю величину; дисперсию; долю единиц, обладающих значением изучаемого признака; дисперсию доли;

· рассчитать ошибки выборки;

· распространить результаты выборки на генеральную совокупность путем определения доверительных интервалов, в которых с определенной вероятностью можно гарантировать нахождение характеристик генеральной совокупности.

Для определения характеристик выборочной совокупности, воспользуемся результатами расчетов п.5 задания, в котором определили, что:

средняя величина капитала составляет:

дисперсия равна:

Доля банков, у которых капитал превышает среднюю величину, для выборочной совокупности определяется по первичным данным таблицы №1. Число таких банков равно 13, тогда их доля в выборочной совокупности составляет:

Дисперсия доли рассчитывается, как произведение значения доли на дополнение ее до единицы, т.е.: . Тогда, дисперсия доли составляет:

Для расчета ошибок выборки можно воспользоваться формулами для бесповторного отбора, т.к. из условия задания можно определить численность генеральной совокупности. Тогда, средняя ошибка выборки для средней величины:

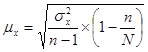
где		дисперсия выборочной совокупности
	численность единиц выборочной совокупности
	численность единиц генеральной совокупности

Т.к. , что по условию составляет 5% от численности генеральной совокупности, то , тогда средняя ошибка выборки для средней величины:

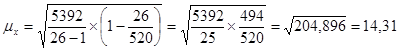
Предельная ошибка для средней величины рассчитывается по формуле:

где		средняя ошибка выборки для средней величины
	коэффициент доверия

Коэффициент доверия принимается в зависимости от уровня доверительной вероятности и числа степеней свободы. Для малой выборки (меньше 30 единиц) определяется по таблице Стьюдента.