Математика / Реферат: Структура сходящихся последовательностей

Реферат: Структура сходящихся последовательностей

из этого неравенства следует, что при n³N выполняется неравенство |y_n |>. Поэтому при n³N имеем . Следовательно, начиная с этого номера N, мы можем рассматривать последовательность , и эта последовательность ограничена. Лемма доказана.

ТЕОРЕМА: Частное двух сходящихся последовательностей {x_n } и {y_n } при условии, что предел {y_n } отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {x_n } и {y_n }.

Доказательство: Из доказанной ранее леммы следует, что, начиная с некоторого номера N, элементы последовательности {y_n } отличны от ноля и последовательность ограничена. Начиная с этого номера, мы и будем рассматривать последовательность . Пусть а и b – пределы последовательностей {x_n } и {y_n }. Докажем, что последовательность 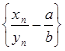бесконечно малая. В самом деле, так как x_n =а+a_n , y_n =b+b_n , то

.
Так как последовательность ограничена, а последовательность бесконечно мала, то последовательность 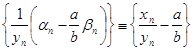бесконечно малая. Теорема доказана.

Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.

ТЕОРЕМА: Если элементы сходящейся последовательности {x_n }, начиная с некоторого номера, удовлетворяют неравентству x_n ³b (x_n £b), то и предел а этой последовательности удовлетворяет неравенству а³b (a£b).

Доказательство: Пусть все элементы x_n , по крайней мере начиная с некоторого номера, удовлетворяют неравенству x_n ³b. Предположим, что а<b. Поскольку а – предел последовательности {x_n }, то для положительного e=b-a можно указать номер N такой, что при n³N выполняется неравенство

|x_n -a|<b-a.

Это неравенство эквивалентно

-(b-a)<x_n -a<b-a

Используя правое из этих неравенств мы получим x_n <b, а это противоречит условию теоремы. Случай x_n £b рассматривается аналогично. Теорема доказана.

Элементы сходящейся последовательности {x_n } могут удовлетворять строгому неравенству x_n >b, однако при этом предел а может оказаться равным b. Например, если x_n =1/n, то x_n >0, однако .

Следствие 1: Если элементы x_n и у_n у сходящихся последовательностей {x_n } и {y_n }, начиная с некоторого номера, удовлетворяют неравенству x_n £ у_n , то их пределы удовлетворяют аналогичному неравенству

Элементы последовательности {y_n -x_n } неотрицательны, а поэтому неотрицателен и ее предел . Отсюда следует, что

Следствие 2: Если все элементы сходящейся последовательности {x_n } находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте.

Это выполняется, так как а£x_n £b, то a£c£b.

ТЕОРЕМА: Пусть {x_n } и {z_n }- сходящиеся последовательности, имеющие общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {y_n }удовлетворяют неравенствам x_n £y_n £z_n . Тогда последовательность {y_n } сходится и имеет предел а.

Доказательство: достаточно доказать, что {y_n -a} является бесконечно малой. Обозначим через N’ номер, начиная с которого, выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполнятся также неравенства x_n -а £ y_n -а £ z_n -а. Отсюда следует, что при n³N’ элементы последовательности {y_n -a} удовлетворяют неравенству

|y_n -a| £ max {|x_n -a|, |z_n -a|}.

Так как и , то для любого e>0 можно указать номера N₁ и N₂ такие, что при n³N₁ |x_n -a|<e, а при n³N₂ |z_n -a|<e. Итак последовательность {y_n -a} бесконечно малая. Теорема доказана.

Итак, мы показали неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.

ПРИМЕРЫ

1. Последовательность сходится и имеет своим пределом ноль. Ведь каково бы ни было e>0, по свойству Архимеда вещественных чисел существует такое натуральное число n_e , что n_e >. Поэтому для всех n³n_e , а это означает, что .