Реферат: Сущность теории вероятностей

Отказы элементов при передаче информации - события независимые. Известны вероятности передачи информации об угрозе i-м элементом, Pi (i=1,…,8).

Найти вероятность доведения информации о поступившей экономической угрозе до руководства фирмы.

Дано: Р1=Р2=Р8=0.69; Р3=Р4=Р6=0.84; Р5=Р7=P9=0.79

Найти: Р(А)-?

Решение:

Обозначим событие А – исправность системы

событие А1 – безотказная работа элемента 1

событие А2 – безотказная работа элемента 2

событие А3 – безотказная работа элемента 3

событие А4 – безотказная работа элемента 4

событие А5 – безотказная работа элемента 5

событие А6 – безотказная работа элемента 6

событие А7 – безотказная работа элемента 7

событие А8 – безотказная работа элемента 8

гипотеза H1 – элементы 5 и 6 работают

гипотеза Н2 – элементы 5 и 6 не работают

гипотеза Н3 – элемент 5 работает, а 6 не работает

гипотеза Н4 – элемент 5 не работает, а 6 работает

Рассмотрим систему и бозначим ее за систему В

Используем метод разложения систему по базисному элементу, основанное на теореме о полной вероятности.

1) Пусть имеет место гипотеза Н1 и 5 и 6 элементы работают, тогда

7

2

1

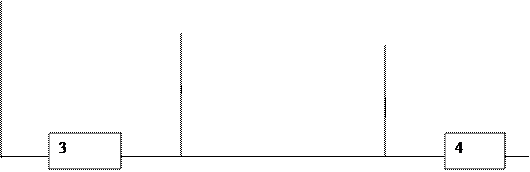
Найдем вероятность исправности данной системы:

Р(Н1)=Р(А5)*Р(А6)=0.6636

Р(B/H1)=P[(A1+A3)*(A7+A4)*A2]*P(H1)=(P1+P3-P1*P3)*P2*(P7+P4-P7*P4)*P(H1)=(0.69+0.84-0.5796)*0.69*(0.79+0.84-0.6636)*0.6636= =0.655776*0.6413034=0.4205