Реферат: Сущность теории вероятностей

Р(А)=Р[(P8*P9)+(P*P9)]=P8*P9+ P*P9 - P8*P9* P*P9=0.5451+0.5282-0.29=0.7833

Ответ:

Вероятность доведения информации о поступившей экономической угрозе до руководства фирмы равна 0.7833

Задание 4

Инвестор вложил капитал в ценные бумаги двух финансовых фирм. При этом он надеется получить доход в течение обусловленного времени от первой фирмы с вероят­ностью P₁ ; от второй — с вероятностью P₂ . Однако есть возмож­ность банкротства фирм независимо друг от друга, которая оце­нивается для первой фирмы вероятностью P₃ ; для второй — P₄ . В случае банкротства фирмы инвестор получает только вложенный капитал. Какова вероятность того, что инвестор по­лучит прибыль?

Дано: Р₁ =0,95; Р₂ =0,90; Р₃ =0,09; Р₄ =0,01

Найти: Р(А)-?

Решение:

Обозначим Р(А) – вероятность того, что инвестор получит прибыль.Всего 3 возможных варианта получения прибыли:

1.получение прибыли и с первого предприятия и со второго(Р1*Р2)

2.получения прибыли с первого, а со второго нет(Р1*Р4)

3.получения прибыли со второго, а с первого нет(Р2*Р3)

Используем теорему сложения вероятностей для трех совместных событий:

P(A)=P[(P1*P3)+(P2*P3)+(P1*P4)]=P1*P2+P2*P3+P1*P4-P1*P2*P2*P3-P1*P2*P1*P4-P1*P4*P2*P3+P1*P2*P2*P3*P1*P4=0.855+0.081+0.0095-0.0693-0.0082-0.0008+0.00065=0.867895

P(A)=0.8697

Ответ:

Вероятность того, что инвестор, получит прибыль равна 0,8679

Задание 5

Случайная величина – годовой доход наугад взятого налогоплательщика. Плотность распределения вероятностей случайной величины задана в виде:

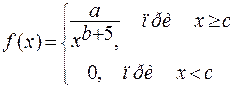
где a – неизвестный параметр распределения, а величины b и c являются константами, значения которых заданы в таблице вариантов задания.

Требуется :

1) Определить значения параметра «а» и построить график функции f (х).

2) Найти функцию распределения F (х) и построить её график.

3) Определить математическое ожидание m _x , дисперсию D _x и среднее квадратическое отклонение годового дохода .

4) Вычислить значения третьего µ ₃ и четвертого µ ₄ центральных моментов, и определить коэффициенты ассиметрии А s и эксцесса Ex .

5) Определить размер годового дохода Х₁ в тыс. у.е., не ниже которого с вероятностью Р окажется годовой доход случайного выбранного налогоплательщика.

Дано:

с=0,7

b=0,30

P=0,55

Найти: 1) a-? f(x)-?