Реферат: Теоремы Перрона-Фробеніуса та Маркова

3. Всі елементи цих рядків додатні.

Доведення теореми для 2х2 матриць.

Запишемо стохастичну матрицю у вигляді , де

Запишемо її характеристичне рівняння: ,

Це квадратне рівняння з дискрімінантом:

І тому

З урахуванням маємо , але якщо , то це значить, що p =q =1 або p =q =0, відкіля матриця P буде мати вигляд , або і тоді P ⁿ містить нулі , що суперечить умові. Таким чином .

Беспосередньою перевіркою з урахуванням стохастичності встановлюємо, що власному значенню відповідає власний вектор , де x ₁ =x ₂ , тобто, наприклад власний вектор. Знайдемо власний вектор , що відповідає власному значенню .

За визначенням

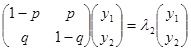
Звідки

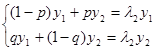
Згадуючи, що отримуємо

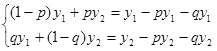
Очевидно, що рівняння системи пропорційні, тому одне з них можна відкинути. Знайдемо y ₁ з першого рівняння: або звідки , але , бо в протилежному випадку дана матриця мала б вигяд: , а тоді матриця мала б нульовий елемент , що суперечить умові. Тому можна записати, що

Доведемо тепер твердження 1 теореми.

Розглянемо матрицю S, стовпцями якої є власні вектори матриці P. Нам необхідно отримати зручну формулу для Pⁿ .

Позначимо .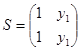

Оскілки , то існує S^- 1. Перепишемо рівняння та 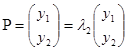у матричній формі

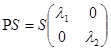або .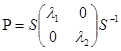

Відкіля 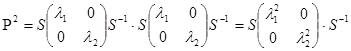і взагалі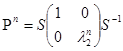

Знайдемо границю Pⁿ :

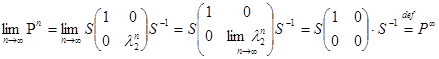
Твердження 1 теореми доведено.

Доведемо тепер, що рядки матриці однакові. Для цього обчиcлимо .

Оскільки , то 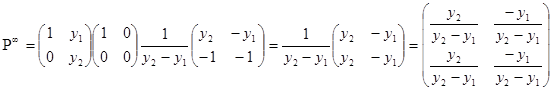Ми бачимо, що рядки матриці - однакові. Доведемо тепер, що їх елементи додатні. Для цього врахуємо отриману раніше залежність