Реферат: Типовые динамические звенья и их характеристики

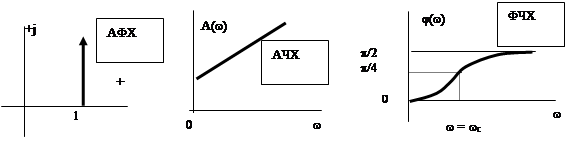
Частотные характеристики звена (рис. 27а-в) определяются соотношениями:

1

а) б) в)

Рис. 27

Логарифмические частотные характеристики звена (рис. 28) определяются по формуле:

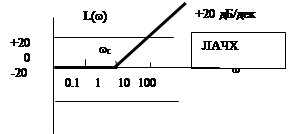Рис. 28

Форсирующее звено 2-го порядка. Передаточная функция форсирующего звена 2-го порядка имеет вид:

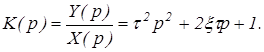(15)

Логарифмические частотные характеристики звена имеют вид:

Запаздывающее звено. Дифференциальное уравнение и передаточная функция запаздывающего звена имеют вид:

(16)

(17)

где t – время запаздывания.

В соответствии с теоремой запаздывания . При этом переходная функция звена и его функция веса (рис. 30а, б) соответственно определяются соотношениями:

Рис. 30

Частотные характеристики звена (рис. 31а-в) определяются соотношениями:

а) б) в)

Рис. 31

Устойчивые и неустойчивые звенья. В устойчивых звеньях переходный процесс является сходящимся, а в неустойчивых он расходится. Устойчивые звенья называются минимально – фазовыми. Эти звенья не содержат нулей и полюсов в правой полуплоскости корней. Неустойчивые звенья называются не минимально – фазовыми. Т. е. изменению амплитуды на ±20 дБ/дек соответствует изменение фазы на ±p/2, а ±40 дБ/дек – на ±p.

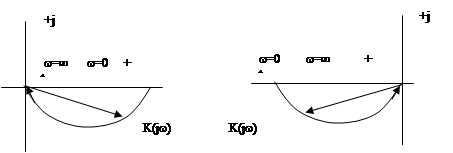
Пример 1. Построить частотные характеристики для звеньев

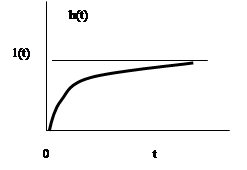
Для заданных передаточных функций звеньев, характеристики имеют вид (рис. 32):

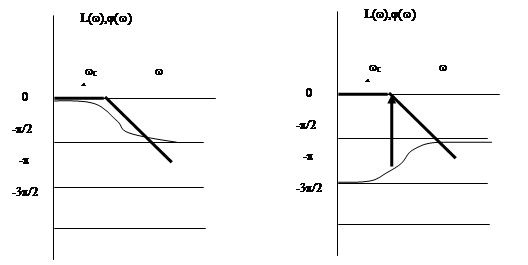Рис. 32

Идеальные и реальные звенья. Идеальные звенья физически не реализуемы, реальные звенья содержат инерционности.

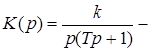реальное интегрирующее звено;