Реферат: Тождественные преобразования показательной и логарифмической функций

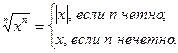
Замечание 2. Удобно считать, что корень первой степени из числа равен . Корень второй степени из числа называют квадратным корнем , а корень третьей степени называют кубическим корнем .

Напомним известные свойства арифметических корней -ой степени.

Для любого натурального , целого и любых неотрицательных целых чисел и справедливы равенства:

1. .

2. .

3. .

4.

5. .

Перейдём к введению степени с рациональным показателем.

Выражение определено для всех и , , кроме случая при . Напомним свойства таких степеней.

Для любых чисел , и любых целых чисел и справедливы равенства:

Отметим так же, что если , то при и при

Определение: Степенью числа с рациональным показателем , где – целое число, а – натуральное , называется число .

Итак, по определению .

При сформулированном определении степени с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (разница заключается в том, что свойства верны только для положительных оснований).

§2. Показательная функция.

Это функция вида (,). Для неё , , , и при график имеет такой вид:

При вид графика такой:

1. Число называется основанием показательной функции. Область определения функции – вся числовая прямая.

2. Область значения функции – множество всех положительных чисел.

3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле

(a ^x )¢ =a ^x lna

4. При а >1 функция монотонно возрастает, при а <1 монотонно убывает.

5. Показательная функция имеет обратную функцию, называемую логарифмической функцией.

6. График любой показательной функции пересекает ось 0y в точке y =1.

7. График показательной функции – кривая, направленная вогнутостью вверх.

8. При любых действительных значениях и справедливы равенства

Эти формулы называют основными свойствами степеней.

Можно так же заметить, что функция непрерывна на множестве действительных чисел.

§3. Логарифмическая функция.