Реферат: Центральная Предельная Теорема и её приложения. Решение Определенного интеграла методом Монте-Карло

Основные непрерывные распределения

Определение. Случайная величина ξ называется равномерно распределено в интервале (a, b), если её плотность распределения постоянная, т.е. f(x) = с.

Из 3 – го свойства плотности имеем:

Итак,

Изобразим график плотности распределении.

(Рис.1.)График функции плотности распределения

Функция распределения согласно (1) и учитывая свойства будет:

Изобразим график функции распределения.

Нормальное распределение

Нормальное распределение – это наиболее важное распределение, которое встречается в почти и везде.

Любая случайная величина, которая формируется, как результат суммарного воздействия многих других случайных величин каждое из которых вносит вклад распределена нормально.

Определение. Говорят, что ξ имеет нормальное распределение с параметрами а и σ , где а Î R, σ > 0, и пишут ξ Î N(а, σ) если ξ имеет следующую плотность распределения:

для любого x Î R.

Функцию распределения этого закона можно записать лишь в таком виде:

ЗАКОН БОЛЬШИХ ЧИСЕЛ

Закон больших чисел Чебышева. Имеет место, следующее утверждение. Пусть последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т.е. для любого i. Тогда, каково бы нибыло, ε>0 справедливо соотношение

Доказательство:

Обозначим через величину , т.е. среднюю арифметическую n случайных величин. Случайная величина имеет математическое ожидание

и дисперсию

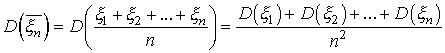
(здесь мы воспользовались свойствами математического ожидания и дисперсии). Применяя к случайной величине вторую лемму Чебышева, найдем, что