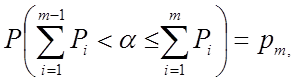Реферат: Центральная Предельная Теорема и её приложения. Решение Определенного интеграла методом Монте-Карло

т.е.

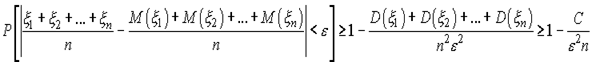
так как при любом i, и следовательно,

Учитывая, что вероятность любого события не превосходит единицы, получим

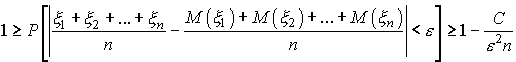
Переходя к пределу при , имеем

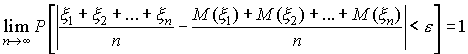
Смысл закона больших чисел Чебышева состоит в следующем. В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.

Неравенство Чебышева.

Пусть ξ случайная величина с Mξ и Дξ. Тогда для этой случайной величины выполняется неравенство

- Неравенство Чебышева.

Другим видом неравенства Чебышева является

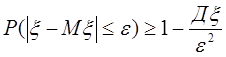
В качестве ε берем 3σ = 3. Получаем: 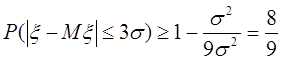- правило “Трех Сигм”.

Центральная предельная теорема

Центральная Предельная Теорема: Пусть последовательность независимых, одинаково распределенных с.в. с конечной дисперсией. Обозначим и . Тогда

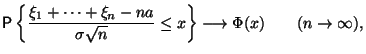
где -- функция распределения стандартного нормального закона.

Замечание 1. Обозначим . Тогда , . Следовательно, утверждение ЦПТ может быть записано в виде

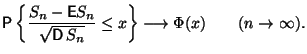
ЦПТ имеет огромное значение для применений теории вероятностей в естествознании и технике. Ее действие проявляется там, где наблюдаемый процесс подвержен влиянию большого числа независимых случайных факторов, каждый из которых лишь ничтожно мало изменяет течение процесса. Наблюдатель, следящий за состоянием процесса в целом, наблюдает лишь суммарное действие этих факторов. Эта схема поясняет также исключительное место, которое нормальное распределение занимает среди других вероятностных распределений.

Моделирование случайных величин

Определение. Получение значений случайной величины заданными законами распределения называется моделированием случайной величины.

Стандартный метод моделирования дискретной случайной величины.

Допустим имеется дискретная случайная величина заданная таблицей :

ξ	X1	X2	...	Xm	…
P1	P2	…	Pm	…

Σpi = 1;

Стандартный метод моделирования такой случайной дискретной величины основан на следующем соотношении: