Реферат: Центральная Предельная Теорема и её приложения. Решение Определенного интеграла методом Монте-Карло

где α равномерная на [0, 1] случайная величина. Pm соответствует хm.На этом и основывается стандартный метод. Из соотношения (*) вытекает следующий простой алгоритм моделирования дискретной случайной величины, который называется стандартным алгоритмом.

Берем случайную величину α, равномерную в [0, 1] , например, с помощью стандартной процедуры Random.

Надо определить промежуток или интервал в который попадает случайная величина α.Пусть номер этого промежутка или интервала равно m. Если этот номер равно m, то ξ пнимет значение хm

m=0, s=0;

α=random;

m=m+1; s=s+pm

Если α<s то переходим на (f)

Иначе на (с)

x=xm

Метод Монте-Карло для вычисления определенных интегралов

Метод Монте-Карло занимает особое положение среди методов вычисления определенных интегралов по двум причинам. Во-первых, это единственный метод, позволяющий вычислять интегралы высокой кратности. И во-вторых, это метод, который дает лишь вероятностные гарантии степени точности вычисления интегралов.

Метод Монте-Карло - это статистический метод, его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации и массового обслуживания, при исследовании сложных систем (экономических, биологических и т. д.).

Сущность метода состоит в том, что в решаемую задачу вводят случайную величину ξ, изменяющуюся по какому-то закону p(ξ). Как правило, случайную величину выбирают таким образом, чтобы искомая в задаче величина стала математическим ожиданием от случайной величины.

Таким образом мы определяем искомую величину лишь теоретически. А вот чтобы найти ее численно, пользуются статистическими методами: берут выборку случайной величины ξ объемом элементов. В результате получают вариант случайной величины ξi, для которых вычисляют их среднее арифметическое (выборочное среднее)

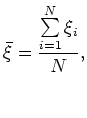
которое и принимают в качестве приближенного значения (оценки) искомой величины :

Для получения результата приемлемой точности по методу Монте-Карло требуется большое число статистических испытаний. Именно поэтому этот метод иногда так и называют: метод статистических испытаний.

Теория метода Монте-Карло изучает способы выбора случайных величин ξ для решения различных задач, а также способы уменьшения дисперсии используемых случайных величин. Уменьшение дисперсии играет большую роль, поскольку при равных объемах выборок, выборка с меньшей дисперсией имеет меньшую погрешность.

Итак, для вычисления однократного интеграла методом Монте-Карло может быть применена формул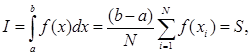а

(а)

где xi равномерно распределенное на интервале [a, b] случайное число. Справедлива следующая оценка точности вычисления интеграла по формуле (а) с вероятностью p=1-η выполняется неравенство

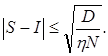
Например, если положить p=99%, тогда η = 0.01 и можно утверждать, что с вероятностью 99% справедливо неравенство

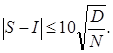
где

Все, что нужно для вычисления интегральной суммы по формуле (1) - это научиться получать случайные числа, равномерно распределенные на интервале [a, b]. Для этой цели можно использовать генератор случайных чисел, входящий в состав стандартных библиотек, поставляемых с компилятором. С помощью функции random легко получить случайное вещественное число, равномерно распределенное на интервале [0, 1] - например, результатом выполнения оператора x=random является случайное вещественное число из интервала [0, 1]. Имея случайное вещественное число из интервала [0, 1] легко получить случайное число из любого интервала. Например, если z - случайное число из интервала [0, 1] , тогда x=a+(b-a)*z - случайное число из интервала [a, b].