Реферат: Центральная Предельная Теорема и её приложения. Решение Определенного интеграла методом Монте-Карло

Метод Монте-Карло легко обобщается на интегралы произвольной кратности. Например, двукратный интеграл может быть вычислен по формуле

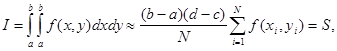
где xi, yi - случайные числа, равномерно распределенные на интервалах [a, b] и [c, d] соответственно. Оценка точности вычисления интеграла по формуле (b) совершенно аналогично приведенной выше для случая однократного интеграла и поэтому здесь не приводится.

Пример №1: Вычислить определенный интеграл I =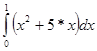

Решение.

= .

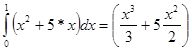Точное значение интеграла I=, ниже приведены результаты программы.

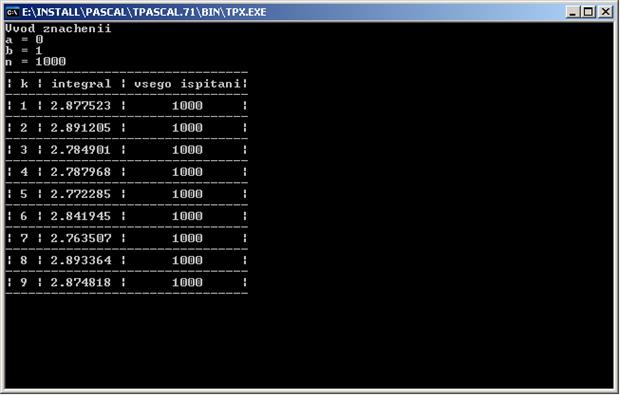
Листинг программы приведен в приложении №1. Программа называется MonteKarlo.

Пример №2: Вычислить определенный интеграл I =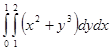

Решение.

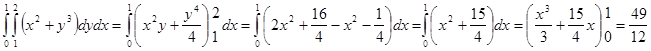
Точное значение интеграла I=, ниже приведены результаты программы.

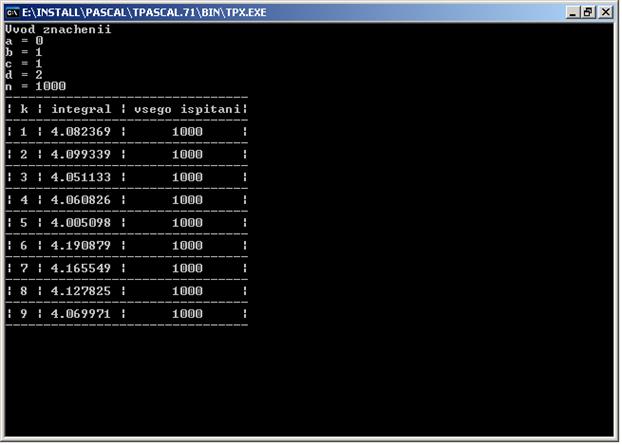
Листинг программы приведен в приложении №2. Программа называется MonteKarlo1.

Приложение №1.

Программа вычисления одномерного определенного интеграла методом Монте-Карло.

program MonteKarlo;

uses crt;

Label l1, l2;

var

j1, j, a, b, c, n1, k, n:integer;

I, Y, x:real;

Begin

randomize;

clrscr;

writeln('Vvod znachenii');

write('a = ');

Read(a);