Реферат: Цепи постоянного тока

Для контура рис 1.7 это выражение будет иметь вид:

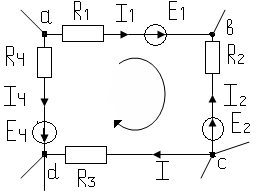
Рис. 1.7

Второй закон Кирхгофа описывает тот факт, что при обходе контура и возвращении в конечную точку, потенциал этой точки не мажет измениться, так - как иначе не соблюдался бы закон сохранения энергии.

11 Эквивалентные преобразования пассивных участков электрической цепи

В зависимости от назначении электрической цепи, её элементы могут соединяться между собой последовательно, параллельно, последовательно – параллельно (по смешанной схеме), треугольником или звездой.

Последовательным называют соединение при котором ток в каждом элементе один и тот же. При таком соединении “n” резисторов (рис. 1.8а) могут быть заменены одним резистором (рис. 1.8б) с эквивалентным сопротивлением Rэ, при котором ток I в обоих схемах будет одинаков (при равенстве напряжения U на входах схем).

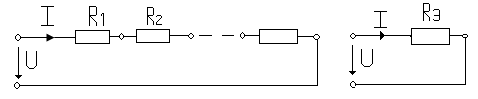
а) б)

рис. 1.8

Для схемы рис. 1.8а)

,

а для схемы рис. 1.8б)

Таким образом (из равенства напряжений на входах) получаем, что:

(1.1.19)

Эквивалентное сопротивление последовательного соединения резисторов равно сумме сопротивлений этих резисторов.

Параллельным называют соединение при котором все участки цепи присоединяются к одной паре узлов, т.е. находятся под воздействием одного и того же напряжения. При таком соединении рис. 1.9а) “n” параллельных резисторов можно заменить одним эквивалентным рис. 1.9б) сопротивление RЭ которое обеспечивает равенство токов I.

В неразветвлённых участках цепи:

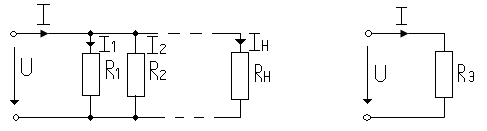
Рис.1.9.

Для схемы рис.1.9(а) по первому закону Кирхгофа можно записать:

Так как для каждой ветви по закону Ома

,то :

, или

(1.1.20)

Поскольку

; ; ,…,

То окончательно получаем:

(1.1.21)

Эквивалентная проводимость параллельно соединённых резистивных элементов равна сумме проводимостей этих элементов.

Из (1.20) следует, что при параллельном соединении двух резисторов их общее (эквивалентное) сопротивление равно:

(1.1.22)