Реферат: Цепи постоянного тока

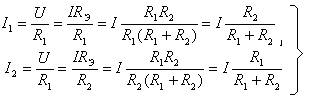(1.1.23)

Сопротивления (1.1.23) называют формулами и разброса токов. Они могут быть получены также из системы уравнений:

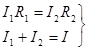(1.1.24)

Смешанное (последовательно-параллельное) соединение резистивных элементов приведено на рис.1.11

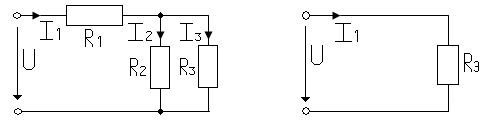
Рис.1.11

Из рис. 1.11 следует, что величина электрического сопротивления ,при котором ток в обоих схемах одинаков, равна :

(1.1.25)

Соединение треугольником и звездой .

В некоторых электрических цепях встречаются соединения элементов, которые нельзя отнести ни к одному из выше рассмотренных. Пример такой цепи приведён на рис.1.22(а):

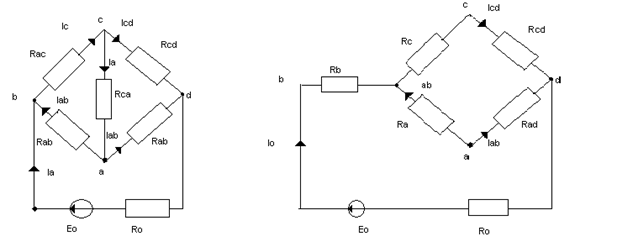
а) б)

рис.1.12

Резисторы Rab, Rbc и Rcd на рис.1.12(а) соединены треугольником, а на рис. 1.22 (б) резисторы Ra, Rb, Rc - соединены звездой. Схема рис.1.12(б) проще для расчёта,чем схема рис.1.12(а),поэтому следует получить выражение Ra, Rb, Rc через Rab, Rbc, Rca и наоборот.

При эквивалентной замене обоих схем, токи Ia, Iab, Icd равны и, следовательно, равны напряжения Uab, Ubc, Ucd.

Запишем уравнение по второму закону Кирхгофа для треугольника abc рис.1.12(а):

(1.1.26)

Для узлов a и b в треугольнике по первому закону Кирхгофа:

, (1.1.27)

Подставив (1.27) в (1.26),получим:

(1.1.28)

Для звезды рис.1.12 (б):

(1.1.29)

Из сравнения (1.28) с (1.29) следует, что:

; (1.1.30)

По аналогии можно получить, что:

(1.1.31)

Формулы (1.30) И (1.31) позволяют преобразовать треугольник сопротивлений в эквивалентную звезду сопротивлений.

Формулы обратного перехода звезды сопротивлений в треугольник сопротивлений можно получить заменив в формулах (1.30) и (1.31) все сопротивления проводимостями. При этом получим:

; ; (1.1.32)

Переходя к сопротивлениям, получим:

; ; ; (1.1.33)

12 Расчёт электрической цепи постоянного тока с одним источником ЭДС

Метод эквивалентных преобразований (МЭП).