Реферат: Цепные дроби
Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава I. ПРАВИЛЬНЫЕ КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
§1 . Представление рациональных чисел цепными дробями
§2. Подходящие дроби. Их свойства. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава II. БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ
§ 1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями
1.1. Разложение действительного иррационального числа в правильную бесконечную цепную дробь . . . . . . . . . . . . . . . . . . . . .
1.2. Сходимость правильных бесконечных цепных дробей. . . . .
1.3. Единственность представления действительного иррационального числа правильной бесконечной цепной дробью
§2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя
2.1. Оценка погрешности при замене действительного числа его подходящей дробью. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Приближение действительного числа подходящими дробями
2.3. Теорема Дирихле. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4. Подходящие дроби как наилучшие приближения
§3. Квадратические иррациональности и периодические цепные дроби. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§4. Представление действительных чисел цепными дробями общего вида . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Решение задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Используемая литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Введение
Целью моей курсовой работы является исследование теории цепных дробей. В ней я попытаюсь раскрыть свойства подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности, которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.
Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.
Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.
Глава I. Правильные конечные цепные дроби.
§1. Представление рациональных чисел цепными дробями.
Целое число, являющееся делителем каждого из целых чисел ![]() , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
, называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
Пусть ![]() - рациональное число, причем b >0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
- рациональное число, причем b >0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:
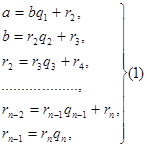
где неполным частным последовательных делений![]() соответствуют остатки
соответствуют остатки![]() с условием b>
с условием b>![]() >
>![]() >…>
>…>![]() >0, а соответствует остаток 0.
>0, а соответствует остаток 0.
Системе равенств (1) соответствует равносильная система
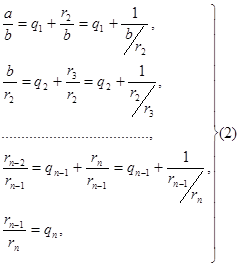
из которой последовательной заменой каждой из дробей![]() и т.д. ее соответствующим выражением из следующей строки получается представление дроби
и т.д. ее соответствующим выражением из следующей строки получается представление дроби![]() в виде:
в виде:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--