Реферат: Цепные дроби

7. Теорема: Расстояние между двумя соседними подходящими дробями .

Доказательство: Так как , то , что и требовалось доказать.

Глава II. Бесконечные цепные дроби.

§1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями.

1.1 Разложение действительного иррационального числа в правильную бесконечную цепную дробь.

В предыдущей главе мы рассмотрели, как в процессе последовательного выделения целой части и перевертывания дробной рациональная дробь разлагается в конечную непрерывную дробь.

=()

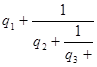(1)

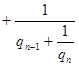
и, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби.

Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.

Для иррационального числа указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.

Выражение 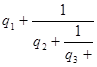(где , ) (2)

возникающее в таком процессе или заданное формально, мы будем называть правильной бесконечной цепной , или непрерывной дробью , или дробью бесконечной длины и обозначать кратко через (), а числа – ее элементами или неполными частными.

Отметим, что разложение возможно только в единственном виде, так как процесс выделения целой части – процесс однозначный.

Рассмотрим пример разложения иррационального числа .

Пусть . Выделим из его целую часть. =3, а дробную часть –3, которая меньше 1, представим в виде , где .

Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:

;

;

.

Если остановиться на этом шаге, то можно записать:

С другой стороны, из формулы для видно, что =3+. Поэтому , вследствие чего, начиная с этого момента, неполные частные станут повторяться.

Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью .

Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической.

Чисто периодическая дробь записывается в виде, а смешанная периодическая в виде .

Итак, разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)).

В общем случае разложения действительного иррационального числа поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после k –го шага, будем иметь: