Реферат: Цепные дроби

так что

.

Числа называются остаточными числами порядкаk разложения . В формуле (4) имеем кусок разложения до остаточного числа .

Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.

Эти дроби называют подходящими дробями . Закон образования соответствующих им простых дробей будет такой же, как и для подходящих дробей в случае конечных непрерывных дробей, так как этот закон зависит только от неполных частных и совершенно не зависит от того, является ли последним элементом или за ним следует еще элемент . Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.

В частности, мы имеем:

1) , причем ;

2) , откуда следует несократимость подходящих дробей ;

3) .

Сравним теперь подходящую дробь и кусок разложения до остаточного числа . Имеем

,

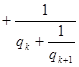
откуда видно, что вычисление по формально производится таким же образом, как вычисление по с тем лишь отличием, что в первом случае заменяется на , а во втором заменяется на . Поэтому на основании формулы можно сделать вывод о справедливости следующего важного соотношения

. (5)

По этой причине мы пишем также , хотя не является здесь целым положительным числом.

При помощи формулы (5) можно вывести следующую теорему и расположении подходящих дробей разложения .

Теорема: Действительное число всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.

Доказательство: Из формулы (5) следует

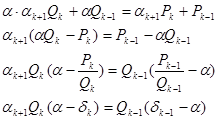
Но , , так что

1) () и () имеют одинаковый знак, а это значит, что находится между и ;

2) , то есть ближе к , чем к .

Теорема доказана.

Так как , то , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:

1) больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;

2) подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального
указанные последовательности являются бесконечными), то есть

(в случае рационального ).

———————————————————

Учитывая то, что при , вследствие чего , переходим к дальнейшему выводу, что в случае иррационального сегменты , , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей , , … и , , … . Но так как принадлежит всем сегментам последовательности, то и совпадает с указанной точкой, так что .