Реферат: Упругие волны
Преимущества такой записи выяснятся в дальнейшем.
§ 4. Волновое уравнение
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (3.6), описывающей плоскую волну. Продифференцировав эту функцию дважды по каждой из переменных, получим
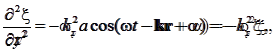 |
???????? ??????????? ?? ??????????? ????
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
 Сопоставив эту сумму с производной по времени и заменивk 2 /ω2 через 1/υ2 (см. (2.7)), получим уравнение
Сопоставив эту сумму с производной по времени и заменивk 2 /ω2 через 1/υ2 (см. (2.7)), получим уравнение
![]() Это и есть волновое уравнение. Его можно записать в виде
Это и есть волновое уравнение. Его можно записать в виде
|
где Δ – оператор Лапласа.
Легко убедиться в том, что волновому уравнению удовлетворяет не только функция (3.6), но и любая функция вида
|

![]() Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем
Действительно, обозначив выражение, стоящее в скобках в правой части (4.4), через ς, имеем
Аналогично
 |
Подстановка выражений (4.5) и (4.6) в уравнение (4.2) приводит к выводу, что функция (4.4) удовлетворяет волновому уравнению, если положить υ=ω/k.
![]() Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при, дает фазовую скоростьэтой волны.
Всякая функция, удовлетворяющая уравнению вида (4.2), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при, дает фазовую скоростьэтой волны.
![]() Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
Отметим, что для плоской волны, распространяющейся вдоль оси х , волновое уравнение имеет вид
|
§ 5. Скорость упругих волн в твердой среде

![]() Пусть в направлении оси х распространяется продольная плоская волна. Выделим в среде цилиндрический объем с площадью основания S и высотой Δx (рис. 5.1). Смещения ξ частиц с разными х в каждый момент времени оказываются различными (см. рис. 1.3, на котором изображено ξ в функции от x ). Если основание цилиндра с координатой х имеет в некоторый момент времени смещениеξ, то смещение основания с координатой x+ Δx будет ξ+Δξ. Поэтому рассматриваемый объем деформируется – он получает удлинение (алгебраическая величина,соответствует сжатию цилиндра) или относительное удлинение. Величина дает среднюю деформацию цилиндра. Вследствие того, что ξменяется с изменением х не по линейному закону, истинная деформация в разных сечениях цилиндра будет неодинаковой. Чтобы получить деформацию ε в сечении х , нужно устремить Δx к нулю. Таким образом,
Пусть в направлении оси х распространяется продольная плоская волна. Выделим в среде цилиндрический объем с площадью основания S и высотой Δx (рис. 5.1). Смещения ξ частиц с разными х в каждый момент времени оказываются различными (см. рис. 1.3, на котором изображено ξ в функции от x ). Если основание цилиндра с координатой х имеет в некоторый момент времени смещениеξ, то смещение основания с координатой x+ Δx будет ξ+Δξ. Поэтому рассматриваемый объем деформируется – он получает удлинение (алгебраическая величина,соответствует сжатию цилиндра) или относительное удлинение. Величина дает среднюю деформацию цилиндра. Вследствие того, что ξменяется с изменением х не по линейному закону, истинная деформация в разных сечениях цилиндра будет неодинаковой. Чтобы получить деформацию ε в сечении х , нужно устремить Δx к нулю. Таким образом,
![]()
![]()
![]()
![]()
(символ частной производной взят потому, что зависит не толькоот x , но и отt ).
![]() Наличие деформации растяжения свидетельствует о существовании нормального напряжения σ, при малых деформациях пропорционального величине деформации. Согласно формуле (14.6) 1-го тома
Наличие деформации растяжения свидетельствует о существовании нормального напряжения σ, при малых деформациях пропорционального величине деформации. Согласно формуле (14.6) 1-го тома
![]()
(E – модуль Юнга среды). Отметим, что относительная деформация , аследовательно, и напряжение σ в фиксированный момент времени зависят от х (рис. 5.2). Там, где отклонения частиц от положения равновесия максимальны, деформация и напряжение равны нулю. В местах, где частицы проходят через положение равновесия, деформация и напряжение достигают максимального значения, причем положительные и отрицательные деформации (т. е. растяжения и, сжатия) чередуются друг с другом. В соответствии с этим, как ужеотмечалось в §1. продольная волна состоит из чередующихся разрежений и сгущений среды.
![]() Обратимся снова к цилиндрическому объему, изображенному на рис.5.1, и напишем для него уравнение движения. Полагая Δx очень малым, проекцию ускорения на ось x можно считать для всех точек цилиндра одинаковой и равной . Масса цилиндра равна ρSΔx , где ρ – плотность недеформированной среды. Проекция на осьx силы, действующей на цилиндр, равна произведению площади основания цилиндра S на разность нормальных напряжений в сечениях (x+ Δx +ξ+Δξ) и (x+ ξ):
Обратимся снова к цилиндрическому объему, изображенному на рис.5.1, и напишем для него уравнение движения. Полагая Δx очень малым, проекцию ускорения на ось x можно считать для всех точек цилиндра одинаковой и равной . Масса цилиндра равна ρSΔx , где ρ – плотность недеформированной среды. Проекция на осьx силы, действующей на цилиндр, равна произведению площади основания цилиндра S на разность нормальных напряжений в сечениях (x+ Δx +ξ+Δξ) и (x+ ξ):
 |
![]() Значение производной в сечении x+ δможно для малых δ представить с большой точностью в виде
Значение производной в сечении x+ δможно для малых δ представить с большой точностью в виде
 |
![]()
где под подразумевается значение второй частной производной ξ по х в сечении х .
Ввиду малосги величинΔx, ξ и Δξпроизведем в выражении (5.3) преобразование (5.4):
 |
![]()
|
|
![]() Подставив найденные значения массы, ускорения и силы в уравнение второго закона Ньютона, получим
Подставив найденные значения массы, ускорения и силы в уравнение второго закона Ньютона, получим
Наконец, сократив на S Δx , придем к уравнению
![]()
![]()
которое представляет собой волновое уравнение, написанное для случая, когда ξ не зависит от у иz . Сопоставление уравнений (4.7) и (5.6) дает, что
![]()
|
![]()
![]() Таким образом, фазовая скорость продольных упругих волн равна корню квадратному из модуля Юнга, деленного на плотность среды. Аналогичные вычисления для поперечных волн приводят к выражению
Таким образом, фазовая скорость продольных упругих волн равна корню квадратному из модуля Юнга, деленного на плотность среды. Аналогичные вычисления для поперечных волн приводят к выражению
![]()
![]()
|