Реферат: Упругие волны

Пусть в некоторой среде распространяется в направлении оси х плоская продольная волна

x = a cos ( wt − kx +a )

Выделим в среде элементарный объем ΔV, настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными, соответственно, и .

Выделенный нами объем обладает кинетической энергией

(ρΔV – масса объема, – его скорость).

Согласно формуле (25.4) 1-го тома рассматриваемый объем обладает также потенциальной энергией упругой деформации

(ε = – относительное удлинение цилиндра, Е — модуль Юнга среды). Заменим в соответствии с (5.7) модуль Юнга через ρυ² (ρ – плотность среды, υ – фазовая скорость волны). Тогда выражение для потенциальной энергии объема ΔV примет вид

Выражения (6.2) и (6.3) в сумме дают полную энергию

Разделив эту энергию на объемΔV, в котором она содержится, получим плотность энергии

w

Дифференцирование уравнения (6.1) один раз по t , другой раз по x дает

Подставив эти выражения в формулу (6.4) и приняв во внимание, что k² υ² = ω² , получим

(6.5)

В случае поперечной волны для плотности энергии получается та­кое же выражение.

(6.6)

?? (6.5) ???????, ??? ????????? ??????? ? ?????? ?????? ??????? ? ?????? ?????? ???????????? ????????. ? ????? ? ??? ?? ????? ????????? ??????? ?????????? ?? ???????? ?? ?????? ????????? ??????. ??????? ???????? ???????? ?????? ????? 1/2. ??????????????? ??????? ?? ??????? ???????? ????????? ??????? ? ??????? ????? ????? ?????

Плотность энергии (6.5) и ее среднее значение (6.6) пропорцио­нальны плотности среды ρ, квадрату частоты ω и квадрату ампли­туды волны а. Подобная зависимость имеет место не только для незатухающей плоскости волны, но и для других видов волн (плос­кой затухающей, сферической и т. д.).

(6.7)

????, ?????, ? ??????? ???????????????? ?????, ???????? ??????????????? ??????? ???????. ??? ??????? ???????????? ?? ?????????? ????????? ? ????????? ????? ????? ????? ??????; ??????????????, ????? ????????? ? ????? ???????. ?????????? ???????, ??????????? ?????? ????? ????????? ??????????? ? ??????? ????????, ?????????? ??????? ??????? ????? ??? ????????????. ???? ????? ?????? ??????????? ??????????? ?? ?????dt ???????dW, ?? ????? ??????? Φ?????

Поток энергии – скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т. е. сов­падает с размерностью мощности. В соответствии с этим Φ измеря­ется в ваттах, эрг/с и т. п.

Поток энергии в разных точках среды может быть различной интенсивности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором пере­носится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Пусть через площадку , перпендикулярную к направлению распространения волны, переносится за время Δt энергия ΔW . Тогда плотность потока энергии равна

(6.8)

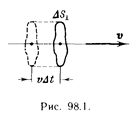
(см. (6.7)). Через площадку(рис. 6.1) будет перенесена за время Δt энергия ΔW , заключенная в объеме цилиндра с основа­ниеми высотой υΔt (υ – фазовая скорость волны). Если размеры цилиндра достаточно малы (за счет малостии Δt ) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то ΔW можно найти как произведение плотности энергииw на объем цилиндра, равный υΔt :

Подставив это выражение в формулу (6.8), получим для плот­ности потока энергии:

(6.9)

(6.10)

(6.11)

(6.12)

Наконец, введя векторv , модуль которого равен фазовой скорости волны, а направление совпадает с направлением распростране­ния волны (и переноса энергии), можно написать

j = w v

Рис.6.2

Рис.6.1

?? ???????? ????????? ??? ??????? ????????? ?????? ????????. ???? ?????? ??? ??????? ?????? ? ???????????? ?????????? ??????? ??????? ?. ?. ?????? ? ?????????? ???????? ?????. ?????? (6.10), ??? ? ????????? ??????? w, ???????? ? ???????????? ???-

странства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно

(см. (6.6)). Выражение (6.11), так же как и (6.6), справедливо для волны любого вида (сферической, затухающей и т. д.).

Отметим, что, когда говорят об интенсивности волны в данной точке, то имеют в виду среднее по времени значение плот­ности потока энергии, переносимой волной.

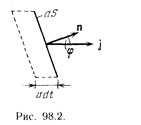
Зная j во всех точках произвольной поверхности S , можно вычислить поток энергии через эту поверхность. С этой целью разо­бьем поверхность на элементарные участкиdS. За время dt через площадку dS пройдет энергия dW, заключенная в изображенном на рис. 6.2 косом цилиндре. Объем этого цилиндра равенdV = υ dt dS cosφ . В нем содержится энергияdW = w dV = w υ dtdS cos φ (w — мгновенное значение плотности энергии в том месте, где рас­положена площадкаdS ). Приняв во внимание, что

w υ dS cos φ = j dS cos φ =j dS

(d S = n dS; см. рис. 6.2), можно написать:dW = j d S dt. Отсюда для потока энергии d Φ через площадку dS получается формула