Реферат: Упругие волны

В соответствии с (11.7) можно сказать, что поток энергии равен потоку вектора j через поверхность S .

Заменив в формуле (6.13) вектор j его средним по времени значением, получим среднее значение Φ:

Вычислим среднее значение потока энергии через произвольную волновую поверхность незатухающей сферической волны. В каж­дой точке этой поверхности векторы j и d S совпадают по направле­нию. Кроме того, модуль вектора j для всех точек поверхности оди­наков. Следовательно,

(r — радиус волновой поверхности). Согласно (6.11) . Таким образом,

(a_r – амплитуда волны на расстоянии r от источника). Поскольку энергия волны не поглощается средой, средний поток энергии че­рез сферу любого радиуса должен иметь одинаковое значение, т. е. должно выполняться условие

Отсюда следует, что амплитуда а, незатухающей сферической волны обратно пропорциональна расстоянию r от источника волны (см. формулу (5.10)). Соответственно средняя плотность потока энергии обратно пропорциональна квадрату расстояния от источника.

В случае плоской затухающей волны амплитуда убывает с рас­стоянием по закону a = = a₀ e^-γx (см. (2.9)). Соответственно средняяплотность потока энергии (т. е. интенсивность волны) убывает по

(6.15)

Здесь c= 2γ – величина, называемая коэффициентом поглощения волны. Она имеет размерность, обратную размерности длины. Легко сообразить, что величина, обратнаяc, равна расстоянию, на котором интенсивность волны уменьшается в е раз.

§ 7. Стоячие волны

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммойколебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции (наложения) волн.

В случае, когда колебания, обусловленные отдельными волна­ми в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Очень важный случай интерференции наблюдается при нало­жении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, образуют стоячую волну.

Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

x₁ = a cos ( wt − kx +a₁ ), x₂ = a cos ( wt + kx +a₂ ).

(7.2)

(7.1)

?????? ?????? ??? ????????? ? ???????????? ????????? ?? ??????? ??? ????? ?????????, ???????

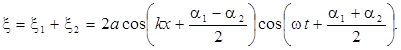Уравнение (7.1) есть уравнение с