Реферат: Упругие волны

Если в каком-либо месте упругой (твердой, жидкой или газо­образной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распро­страняться в среде от частицы к частице с некоторой скоро­стьюυ . Процесс распространения колебаний в пространстве на­зывается волной.

Частицы среды, в которой распространяется волна, не вовле­каются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В попереч­ной волне частицы среды колеблются в направлениях, перпендику­лярных к направлению распространения волны. Упругие попереч­ные волны могут возникнуть лишь в среде, обладающей сопротивле­нием сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.

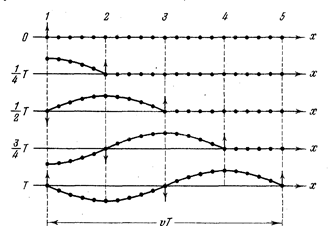На рис. 1.1 показано движение частиц при распространении в среде поперечной волны. Номерами 1, 2 и т. д. обозначены час­тицы, отстоящие друг от друга на расстояние, равное ¼ υ T , т. е. на расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами. В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла час­тицы 1 , вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положе­ния; одновременно начинает смещаться из положения равновесия частица 2 . По прошествии еще четверти периода первая частица будет проходить положение равновесия, двигаясь в направлениисверху вниз, вторая частица достигнет крайнего верхнего положе­ния, а третья частица начнет смещаться вверх из положения рав­новесия. В момент времени, равный Т , первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. Волна к моменту времени Т , пройдя путьυ T , достигнет частицы 5 .

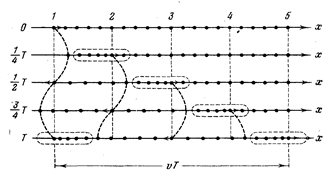На рис. 1.2 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведе­ния частиц в поперечной волне, могут быть отнесены ик данному случаю с заменой смещений вверх и вниз смещениями вправо ивлево. Из рисунка видно,что при распространении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц (места сгущения частиц обведены на рисунке пунктиром), перемещающиеся в направлении распространения волны со ско­ростью υ .

На рис. 1.1 и 1.2 показаны колебания частиц, положения равновесия которых лежат на оси х . В действительности колеблют­ся не только частицы, расположенные вдоль оси х , а совокупность частиц, заключенных в некотором объеме. Распространяясь от ис­точника колебаний, волновой процесс охватывает все новые и но­вые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времениt , называется фронтом волны (или волновым фронтом). Фронт волны пред­ставляет собой ту поверхность, которая отделяет часть простран­ства, уже вовлеченную в волновой процесс, от области, в которой ко­лебания еще не возникли.

Геометрическое место точек,колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую по­верхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых по­верхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют со­бой множество параллельных друг другу плоскостей, в сфериче­ской волне — множество концентрических сфер.

Рассмотрим случай, когда плоская волна распространяется вдоль оси х . Тогда все точки среды, положения равновесия кото­рых имеют одинаковую координату х (но различные значения координат y иz ), колеблются в одинаковой фазе.

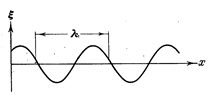На рис.1.3 изображена кривая, которая дает смещение x из положения равновесия точек с различными x в некоторый мо­мент времени. Не следует воспринимать этот рисунок как зримое изображение волны. На рисунке показан график функции x (х , t) для некоторого фиксированного момента времени 1 . С течением времени график перемещается вдоль оси х . Такой график можно строить как для продольной, так и для поперечной волны. В обоих случаях он выглядит одинаково.

(1.1)

?????????? λ , ?? ??????? ???????????????? ????? ?? ?????, ?????? ??????? ????????? ?????? ?????, ?????????? ?????? ?????. ????????, ???

λ =υ T,

где υ — скорость волны, T — период колебаний. Длину волны можно определить также как расстояние между ближайшими точ­ками среды, колеблющимися с разностью фаз, равной 2p (см. рис. 1.3).

(1.2)

??????? ? ??????????? (1.1) T ?????1/v (v ? ??????? ??????????), ???????

λ v =υ .

К этой формуле можно прийти также из следующих соображений. За одну секунду источник волн совершает v колебаний, порождая в среде при каждом колебании один «гребень» и одну «впадину» волны. К тому моменту, когда источник будет завершать v-e коле­бание, первый «гребень» успеет пройти путь υ . Следовательно, v «гребней» и «впадин» волны должны уложиться на длине υ .

§ 2. Уравнения плоской и сферической волн

Уравнением волны называется выражение, которое дает сме­щение колеблющейся частицы как функцию ее координат х , у , z и времени t :

(2.1)

x = x (х, у , z, t)

(имеются в виду координаты равновесного положения частицы). Эта функция должна быть периодической как относительно вре­мени t , так и относительно координат х , y, z . Периодичность по времени вытекает из того, что x описывает колебания час­тицы с координатами х , у , z . Периодич­ность по координатам следует из того, что точки, отстоящие друг от друга на расстоя­ние λ , колеблются одинаковым образом.

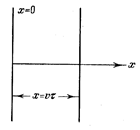
Найдем вид функции x , в случае плос­кой волны, предполагая, что колебания носят гармонический характер. Для уп­рощения направим оси координат так, чтобы ось х совпала с направлением рас­пространения волны. Тогда волновые поверхности будут пер­пендикулярными к оси х и, поскольку все точки волновой поверх­ности колеблются одинаково, смещение x будет зависеть только от х и t : x = x (х , t) . Пусть колебания точек, лежащих в плоскости х = 0 (рис. 2.1), имеют вид

x (х , t) =a cos ( w t + a ) .

Найдем вид колебания точек в плоскости, соответствующей про­извольному значению х . Для того чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время t =x / υ (υ – скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на t от колебаний частиц в плоскости х = 0, т. е. будут иметь вид

x (х , t) =a cos [ w ( t − t ) + a ] = a cos [ w ( t − x / υ ) + a ] .

Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси х, выглядит следующим образом:

(2.2)

x = a cos [ w ( t − x / υ ) + a ]

Величина a представляет собой амплитуду волны. Начальная фаза волны a определяется выбором начал отсчета х и t . При рас­смотрении одной волны начала отсчета времени и координаты обычно выбираются так, чтобы a была равной нулю. При совмест­ном рассмотрении нескольких волн сделать так, чтобы для всех них начальные фазы равнялись пулю, как правило, не удается.

(2.3)

??????????? ?????-???? ???????? ????, ??????? ? ????????? (2.2), ???????

w ( t − x / υ ) + a = const

0,

=

1

υ

??? ????????? ?????????? ????? ????? ???????? t ? ??? ?????? х , ? ??????? ???? ????? ??????????????? ????????. ?????????? ?? ???? ????????dx/dt ???? ????????, ? ??????? ???????????? ?????? ???????? ????. ?????????????????? ????????? (2.3), ???????

υ .

υ .

??????

(2.4)

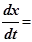
Таким образом, скорость распространения волныυ в уравнении (2.2) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

(2.5)

???????? (2.4)dx/dt > 0. ?????????????, ????????? (2.2) ????????? ?????, ?????????????????? ? ??????? ??????????? х . ?????, ?????????????????? ? ??????????????? ???????????, ??????????? ??????????

x = a cos [ w ( t + x / υ ) + a ]

– υ ,

?????????????, ????????? ????????? ???? ????? (2.5) ? ??????????????????? ???????????? ?????????, ?????? ? ???????????

из которого следует, что волна (2.5) распространяется в сторону убывания х .

(2.6)

,

λ

2π

????????? ??????? ????? ????? ??????? ???????????? ????????????? х ? t ???. ??? ????? ?????? ????????

ω

υ

(2.7)

??????? ?????????? ???????? ??????. ??????? ?????????? ? ??????????? ????????? (2.6) ?? ??????? v , ????? ???????????? ???????? ????? ? ????

(2.8)

(??. ??????? (1.2)). ??????? ? (2.2) ??????? ?????? ? ?????? ?? ???????? (2.7), ?????? ? ?????????? ????????? ??????? ??????, ?????????????????? ????? ??? х:

x = a cos ( w t + kx + a )

Уравнение волны, распространяющейся в сторону убывания х , отличается от (2.8) только знаком при члене kx .

При выводе формулы (2.8) мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При рас­пространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается – наблюдается затухание волны. Опыт показывает, что в однородной среде такое затухание происходит по экспоненциальному закону:a = a ₀ e^–γx . Соответственно урав­нение плоской волны имеет следующий вид:

(2.9)

x = a ₀ e^–γx cos ( w t + kx + a )

(a ₀ – амплитуда в точках плоскости х = 0).

Теперь найдем уравнение сферической волны. Всякий реаль­ный источник волн обладает некоторой протяженностью. Однако если ограничиться рассмотрением волны на расстояниях от источ­ника, значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, по­рождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника равнаw t + a . Тогда точки, лежа­щие на волновой поверхности радиуса r , будут колебаться с фазой

w ( t – r/ υ ) = w t – kr + a

a

(2.10)

(????? ?????? ???? r , ????? ????????? ????? τ =r / υ ). ????????? ????????? ? ???? ??????, ???? ???? ??????? ????? ?? ??????????? ??????, ?? ???????? ?????????? ? ??? ??????? ? ??????????? ??????????? ?? ?????? 1/ r . ?????????????, ????????? ??????????? ????? ????? ???

r

x = cos ( w t + kx + a )

где a — постоянная величина, численно равная амплитуде на рас­стоянии от источника, равном единице. Размерность а равна раз­мерности колеблющейся величины, умноженной на размерность длины.Для поглощающей среды в формулу (2.10) нужно доба­вить множитель e^–γx .

Напомним, что в силу сделанных предположений уравнение (2.10) справедливо только при r , значительно превышающих размеры источника. При стремлении r к нулю выражение для амп­литуды обращается в бесконечность. Этот абсурдный результат объясняется неприменимостью уравнения для малых r .

§ 3. Уравнение плоской волны, распространяющейся в произвольном направлении

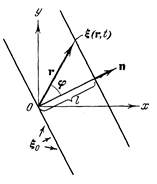Найдем уравнение плоской волны, распространяющейся в на­правлении, образующем с осями координат x , y , z углы α, β, γ. Пусть колебания в плоскости, проходя­щей через начало координат (рис. 3.1), имеют вид

(3.1)

x = a cos ( wt +a )

(3.2)

υ

ω

??????? ???????? ??????????? (??????????), ????????? ?? ?????? ?????????? ?? ?????????? l . ????????? ? ???? ????????? ????? ????????? ?? ????????? (3.1) ?? ????? τ =l /υ:

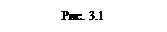
x = a cos [ w( t − ) +a ] =a cos ( wt − kl +a ).

(k =ω/υ; см. формулу (2.7)).

Выразим l через радиус-вектор точек рассматриваемой поверх­ности. Для этого введем единичный вектор n нормали к волновой поверхности. Из рис. 3.1 видно, что скалярное произведение n на радиус-вектор r любой из точек поверхности равно l :

nr = r cos φ=l .

(3.3)

??????? ? (3.2) l ?????nr :

x = a cos ( wt − k nr +a )

(3.4)

??????

k = k n ,

(3.5)

?????? ?? ?????? ????????? ?????k = 2π/λ? ??????? ???????????? ??????? ? ???????? ???????????, ?????????? ????????? ????????. ????? ???????, ????????? (3.3) ????? ??????????? ? ????

x ( r , t ) = a cos ( wt − kr +a )

Мы получили уравнение плоской незатухающей волны, распро­страняющейся в направлении, определяемом волновым векто­ром k . Для затухающей волны нужно добавить в уравнение мно­жительe^{– γl} = e^{– γ nr} .

Функция (3.5) дает отклонение от положения равновесия точ­ки с радиусом-вектором r в момент времени l (r оп­ределяет равновесное положение точки). Чтобы перейти от радиу­са-вектора точки к ее координатам х , у , z , выразим скалярное про­изведение kr через компоненты векторов по координатным осям:

kr = k_x x +k_y y + k_z z .

(3.7)

(3.6)

????? ????????? ??????? ????? ?????? ???

x (x , y , z , t ) = a cos ( wt − k_x x –k_y y – k_z z +a )

2π

λ

cos γ.

2π

λ

cos β,

cos α,

2π

?????

λ

??????? (3.6) ???? ?????????? ????? ? ???????????? х , у , z ? ??????? ??????? t . ? ??????, ????? n ????????? ?e _x , k_x = k , k_y = k_z = 0 (? ????????? (3.6) ????????? ? (2.8). ????? ?????? ?????? ?????????? ??????? ????? ? ????

x = Re ae^{i (ωt -kr +α)}

(3.10)

(3.8)

(3.9)

???? Re ?????? ????????, ????????????, ??? ??????? ?????? ???????????? ????? ???????????????? ?????????. ????? ????, ?????? ??????????? ?????

â = ae ^{i α} ,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--