Реферат: Устойчивость движения в нелинейных системах
Если корни характеристического уравнения расположены в левой полуплоскости, то линеаризованная система устойчива, а соответствующая ей исходная нелинейная система асимптотически устойчива в окрестности, рассматриваемой особой точки.
Если корни расположены в правой плоскости, то линеаризованная система неустойчива, а движение в окрестности особой точки является неустойчивым.
Если корни расположены на мнимой оси, то линеаризованная система не устойчива, а для определения устойчивости нелинейной системы необходимо провести дополнительные исследования нелинейной системы, т.е. уравнения в первом приближении не дают точного представления об устойчивости нелинейной системы.
3. Второй (прямой) метод Ляпунова
Если хотя бы один из корней характеристического уравнения расположен на мнимой оси, то первый метод Ляпунова не дает ответа на вопрос об устойчивости движения в окрестности особой точки, при этом используется второй (прямой) метод Ляпунова, позволяющий определить устойчивость в большом.
Метод основан на использовании специальных функций, называемых функциями Ляпунова. Чтобы выяснить смысл функций Ляпунова рассмотрим фазовый портрет в окрестности некоторой особой точки (рис. 3). Рассмотрим радиус – вектор -r, который изменяется по модулю в функции времени.
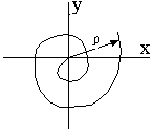
Рис. 3
Если при ![]() , то движение асимптотически устойчиво.
, то движение асимптотически устойчиво.
Если при ![]() увеличивается
увеличивается![]() , то движение не устойчиво.
, то движение не устойчиво.
Если при ![]() const
const![]() , то движение устойчиво в смысле Ляпунова.
, то движение устойчиво в смысле Ляпунова.
Ляпунов доказал, что надо найти такую произвольную функцию H (x, y), которая бы играла роль радиус-вектора r, и была бы положительной для всех точек за исключением, быть может, начала координат, где она может быть равной нулю. Такая функция называется функцией Ляпунова .
Знакоопределенной функцией называется функция, которая при всех значениях аргументов за исключением, может быть, начала координат, где она равна нулю, имеет определенный знак (рис. 4а).
Знакопостоянной функцией называется функция, которая при всех значениях аргументов (за исключением нескольких точек, где она равна нулю) сохраняет постоянный знак (рис. 4б).
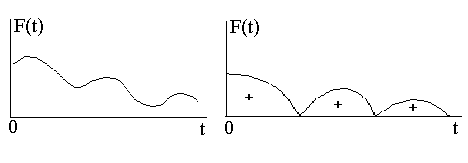
а) б)
Рис. 4
4. Теоремы Ляпунова об устойчивости нелинейных систем
1. Если можно найти такую знакоопределенную функцию H (x, y), что ![]() тоже знакоопределенная функция противоположного знака, то движение в окрестности рассматриваемой особой точки асимптотически устойчиво.
тоже знакоопределенная функция противоположного знака, то движение в окрестности рассматриваемой особой точки асимптотически устойчиво.
2. Если можно найти такую знакоопределенную функцию H (x, y), что ![]() будет знакопостоянной функцией противоположного знака, то движение в окрестности рассматриваемой особой точки будет устойчивым в смысле Ляпунова.
будет знакопостоянной функцией противоположного знака, то движение в окрестности рассматриваемой особой точки будет устойчивым в смысле Ляпунова.
3. Если существует такая функция H (x, y) > 0, что ![]() > 0, то такое движение неустойчиво.
> 0, то такое движение неустойчиво.
Эти теоремы характеризуют достаточные условия устойчивости движения в нелинейных системах. Функции Ляпунова выбираются в виде квадратичных функций или квадратичная функция плюс интеграл исходя из того, что
![]()
 (8)
(8)
Это самое слабое место метода, так как нет способа выбора функций Ляпунова, ее выбор представляет трудности, надо полагаться на интуицию и некоторые рекомендации.
Рассмотрим примеры анализа устойчивости движения в окрестности особых точек с использованием методов Ляпунова.
Пример 1. Пусть задана схема нелинейная система (рис. 5). Определить особые точки и проанализировать их устойчивость, если нелинейные звенья описываются функциями: f(x) = x3 , f(y) = y3 .
 |
Рис. 5
Решение
Запишем дифференциальные уравнения системы