Реферат: Восстановление эталона циклических сигналов на основе использования хаусдорфовой метрики в фазовом пространстве координат

Леонид Соломонович Файнзильберг, к.т.н.

Предложена стохастическая модель порождения циклических сигналов. Показано, что эта модель является обобщением моделей периодической и почти периодической функций. Предложен конструктивный метод оценки эталона по реализации циклического сигнала, наблюдаемого в фазовом пространстве координат.

Введение. Повторяющиеся во времени процессы часто протекают в технических и биологических системах. Такие процессы порождают специфические сигналы, которые в научной литературе принято называть циклическими [1] или квазипериодическими [2]. Типичными примерами циклических сигналов являются электрокардиограмма (ЭКГ), реограмма, магнитокардиограмма и многие другие физиологические сигналы, отражающие циклический характер работы системы кровообращения живого организма.

Известно, что существующие компьютерные системы анализа и интерпретации циклических сигналов, в частности, ЭКГ, все еще не обеспечивают требуемую достоверность результатов [3]. Согласно [4], это в первую очередь вызвано ошибками, которые возникают при измерении параметров (диагностических признаков) при обработке реальных сигналов во временной области. Один из альтернативных методов анализа таких сигналов, предложенный в [5] и получивший развитие в целом ряде других работ, в частности, в

[6-8], предполагает отображение и обработку сигнала в фазовом пространстве координат.

В настоящей статье предлагается модель порождения циклических сигналов и на основе этой модели исследуется новый метод восстановление эталона циклического сигнала по искаженной реализации, наблюдаемой в фазовом пространстве.

Постановка задачи. Пусть наблюдаемый сигнал является результатом искажения периодического процесса случайным возмущением , где - некоторая функция. Назовем эталонным циклом - часть ненаблюдаемой функции на любом из ее периодов . Ставится задача оценить эталон по реализации , наблюдаемой на отрезке .

Стохастическая модель порождения циклических сигналов. Прежде чем переходить к решению поставленной задачи, рассмотрим одну из возможных моделей порождения по эталону. Будем считать, что эталон может быть представлен в виде функции, кусочно-заданной на интервале отдельными фрагментами

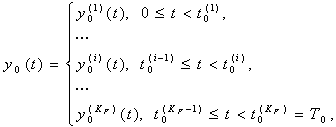(1)

полагая, что число таких фрагментов . Применительно к ЭКГ такие фрагменты соответствуют стадиям процесса возбуждения отдельных участков сердца - деполяризации предсердий (волне), возбуждению (комплексу) и реполяризации (волне ) желудочков [1].

Представим наблюдаемый сигнал в виде последовательности искаженных эталонов (1), предполагая, что на каждом -м цикле такой последовательности () отдельные фрагменты эталона независимо один от другого линейно растягиваются (сжимаются) по времени, а сама функция линейно растягивается (сжимается) по амплитуде. Иными словами, предполагается, что процесс порождения -го фрагмента () каждого -го цикла () осуществляется на основе операторного преобразования

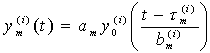, (2)

где - соответственно параметры линейного растяжения (сжатия) по амплитуде и времени, а - сдвиг по времени. Для обеспечения непрерывности порождаемого сигнала предполагается, что Последнее требование всегда можно обеспечить, выполнив предварительную нормировку эталона .

Пусть в пределах каждого -го цикла параметр принимает фиксированное значение

, (3)

где - последовательность реализаций независимых случайных величин, которые с нулевым математическим ожиданием распределены на интервале , ограниченном фиксированным числом .

Предположим также, что параметр принимает фиксированное значение в процессе порождения каждого -го фрагмента -го цикла

, (4)

где - последовательность реализаций независимых случайных величин, которые с нулевым математическим ожиданием распределены на интервалах , ограниченными фиксированными числами .

При таких предположениях продолжительность -го фрагмента -го цикла сигнала связана с продолжительностью соответствующего фрагмента эталона соотношением

.

Следовательно, общая продолжительность -го цикла порождаемого сигнала определяется выражением

,

началу -го цикла соответствует момент времени

,

а началу -го фрагмента -го цикла – момент времени

. (5)

Применим к -му фрагменту эталона операторное преобразование (2), положив параметр сдвига . Тогда из (2) с учетом соотношений (3)- (5) следует, что процесс порождения -го фрагмента на -м цикле можно представить в виде

, (6)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--