Реферат: Восстановление эталона циклических сигналов на основе использования хаусдорфовой метрики в фазовом пространстве координат
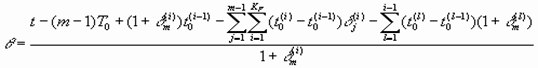 . (7)
. (7)
Предложенная модель, которая описывает неравномерные по времени искажения эталона ![]() , более пригодна для описания реальных циклических сигналов, в частности ЭКГ, нежели ее упрощенный вариант
, более пригодна для описания реальных циклических сигналов, в частности ЭКГ, нежели ее упрощенный вариант
![]() ,
,
полученный в предположении, что фигурирующий в (7) случайный параметр ![]() зависит только от номера
зависит только от номера ![]() цикла, но не зависит от номера
цикла, но не зависит от номера ![]() фрагмента.
фрагмента.
Нетрудно показать, что стохастическая модель (6),(7) является прямым обобщением известных моделей строго периодического и почти периодического процессов. Действительно, положив в (7) ![]() , модель (6) можно представить в виде соотношения
, модель (6) можно представить в виде соотношения
![]() ,
,
которое описывает почти периодический процесс [9], а при дополнительном условии ![]() , сводится к модели строго периодической функции
, сводится к модели строго периодической функции ![]() .
.
Предложенная модель легко может быть обобщена для описания процесса порождения более сложных циклических сигналов, в частности, ЭКГ с изменяющейся морфологией отдельных циклов (экстрасистолами) [10]. Для этого достаточно ввести в рассмотрение не один, а ![]() эталонов
эталонов ![]() , и предположить, что каждый
, и предположить, что каждый ![]() -й цикл порождается путем аналогичных искажений одного из этих эталонов, выбираемых случайным образом в соответствии с вероятностями
-й цикл порождается путем аналогичных искажений одного из этих эталонов, выбираемых случайным образом в соответствии с вероятностями  .
.
Генератор циклических последовательностей. Рассмотрим достаточно простой алгоритм генерации дискретных циклических последовательностей по эталонам. Пусть каждый из ![]() эталонов
эталонов ![]() , (
, (![]() ) представлен конечным числом
) представлен конечным числом ![]() дискретных значений
дискретных значений ![]() , зафиксированных с постоянным шагом квантования по времени. Зададим общее число
, зафиксированных с постоянным шагом квантования по времени. Зададим общее число ![]() фрагментов каждого эталона и номера точек
фрагментов каждого эталона и номера точек ![]() , которые определяют границы
, которые определяют границы ![]() -го и
-го и ![]() -го фрагмента
-го фрагмента ![]() -го эталона.
-го эталона.
При таких исходных данных процедура генерации циклической последовательности сводится к следующим шагам.
Шаг 1. Задаем общее число ![]() циклов генерируемой последовательности.
циклов генерируемой последовательности.
Шаг 2. Определяем число ![]() циклов, порождаемых
циклов, порождаемых ![]() -м эталоном, по формуле
-м эталоном, по формуле ![]() , где здесь и далее
, где здесь и далее ![]() -операция округления до целого числа
-операция округления до целого числа ![]() .
.
Шаг 3. Выбираем номер ![]() эталона, порождающего
эталона, порождающего ![]() -й цикл (
-й цикл (![]() ), по значению реализации
), по значению реализации ![]() целочисленной случайной величины
целочисленной случайной величины ![]() , распределенной на интервале [1,G] т.е.
, распределенной на интервале [1,G] т.е. ![]() =
=![]() .
.
Шаг 4. Если ![]() , то повторяем шаг 3.
, то повторяем шаг 3.
Шаг 5. Определяем число точек ![]() -го фрагмента
-го фрагмента ![]() -го цикла по формуле
-го цикла по формуле
![]() ,
,
где ![]() - реализация случайной величины
- реализация случайной величины ![]() , которая с нулевым математическим ожиданием распределена на интервале
, которая с нулевым математическим ожиданием распределена на интервале ![]() .
.
Шаг 6. По дискретным значениям ![]() -го фрагмента
-го фрагмента ![]() -го эталона в
-го эталона в ![]() узлах любым из методов интерполяции вычисляем значения генерируемой последовательности в
узлах любым из методов интерполяции вычисляем значения генерируемой последовательности в ![]() точках.
точках.
Шаг 7. Модифицируем каждое вычисленное значение ![]() на основе мультипликативной процедуры
на основе мультипликативной процедуры ![]() , где
, где ![]() - реализация случайной величины
- реализация случайной величины ![]() , которая с нулевым математическим ожиданием распределена на интервале
, которая с нулевым математическим ожиданием распределена на интервале ![]() .
.
Шаг 8. Если ![]() , то возвращаемся к шагу 5.
, то возвращаемся к шагу 5.
Шаг 9. Присваиваем ![]() .
.
Шаг 10. Если ![]() , то возвращаемся к шагу 3.
, то возвращаемся к шагу 3.
Результаты моделирования подтверждают эффективность рассмотренного алгоритма для имитации реальных циклических сигналов (рис. 1).

Рис. 1. ЭКГ- сигнал, порожденный моделью (6): по одному эталону (а); по двум эталонам (б)
Метод оценки эталона по искаженной реализации. Пусть циклический сигнал (6) представлен последовательностью ![]() дискретных значений, наблюдаемых в течение
дискретных значений, наблюдаемых в течение ![]() циклов. Предположим, что для каждого
циклов. Предположим, что для каждого ![]() -го значения имеется оценка производной
-го значения имеется оценка производной ![]() . Выполнив нормировку
. Выполнив нормировку
 ,
,
сформируем множество ![]() точек, принадлежащих траектории наблюдаемого сигнала в двумерном нормированном фазовом пространстве
точек, принадлежащих траектории наблюдаемого сигнала в двумерном нормированном фазовом пространстве ![]() .
.
Пусть нам известны номера точек ![]() , соответствующие началам
, соответствующие началам