Реферат: Восстановление эталона циклических сигналов на основе использования хаусдорфовой метрики в фазовом пространстве координат

Будем оценивать расстояние между любыми двумя подмножествами и , хаусдорфовой метрикой [11]

, (8)

где - евклидово расстояние между точками и .

Назовем опорным циклом подмножество векторов , которое имеет минимальное суммарное расстояние (8) с остальными подмножествами

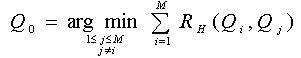, (9)

и будем оценивать эталон (средний цикл) путем усреднения точек различных траекторий, расположенных в окрестности точек опорного цикла.

С этой целью проведем селекцию траекторий, подлежащих усреднению, определив

подмножество тех траекторий, хаусдорфово расстояние которых до опорной меньше заданной величины , т.е. . Для улучшения оценки представим опорный цикл и остальные циклы последовательностью расширенных векторов , которые, помимо нормированных фазовых координат , содержат дополнительную компоненту . Величина вычисляется в каждой -й точке -й траектории по формуле

,

где - номер первой точки -й траектории, состоящей из точек.

Введение дополнительной компоненты позволяет при усреднении точек оценивать их близость не только с точки зрения значений фазовых координат , но и с точки зрения синхронности во времени. Для этого предлагается определять евклидово расстояние между расширенными векторами опорной траектории и расширенными векторами остальных траекторий , а для оценки последовательности точек среднего цикла воспользоваться соотношением

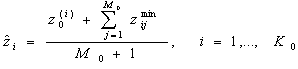, (10)

где - точка, лежащая на -той траектории (не являющейся опорной), которая находится на минимальном евклидовом расстоянии от точки опорной траектории :

.

Последовательность векторов , вычисленная согласно (10), дает оценку ненаблюдаемого эталона в фазовом пространстве, а соответствующая последовательность - оценку эталонного цикла во временной области (рис. 2).

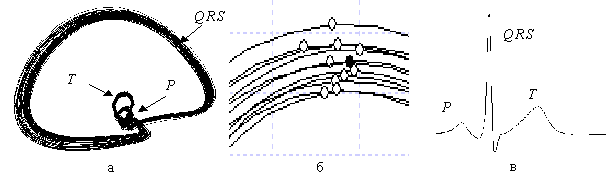
Рис.2. Иллюстрация к алгоритму оценки эталона (на примере ЭКГ) фазовые траектории (а); фрагменты траекторий (б); эталонный цикл (в)

Модельный пример. Пусть эталон имеет форму равнобедренного треугольника (рис. 3 а), заданного двумя фрагментами в виде линейных функций

. (11)

Предположим, что мы наблюдаем два цикла сигнала, порожденного в соответствии с моделью (6) по эталону (11), причем на 1-м цикле параметры растяжения по времени приняли значения и , а на 2-м цикле - и . В результате наблюдаемый сигнал будет описывать функция

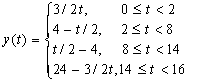, (12)

график которой показан на рис. 3 б).

Совместим наблюдаемые циклы на интервале (рис. 3 в) и усредним их во временной области. Легко видеть, что при этом будет получена оценка (рис 3 г)

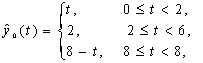
которая по форме не соответствует эталону (рис 3 а). В то же время, усреднение этих же циклов в фазовом пространстве координат (рис. 3 д) с последующим переходом во временную область (рис. 3 е) позволяет точно восстановить эталон (11).

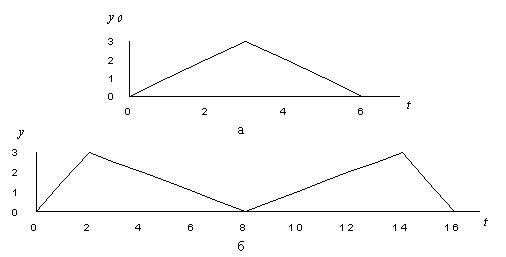
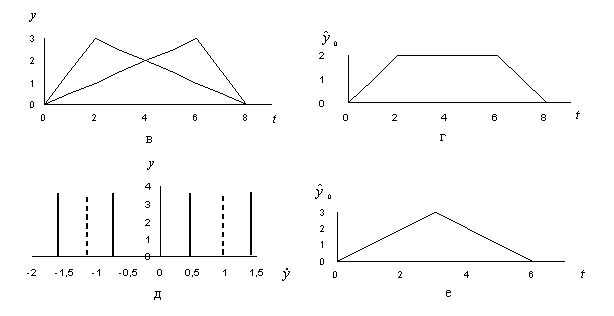
Рис.3. Иллюстрация к модельному примеру

эталон (а); наблюдаемый сигнал (б); совмещенные во времени циклы (в); оценка эталона при усреднении во временной области (г); фазовая траектория (д); оценка эталона при усреднении в фазовом пространстве (е)