Реферат: Вычисление интеграла по поверхности
Содержание
1)Поверхностный интеграл второго рода
2)Вычисление интеграла по поверхности
3)Теорема Остроградского-Гаусса
4)Дивергенция
Литература
интеграл теорема доказательство
Интеграл по поверхности
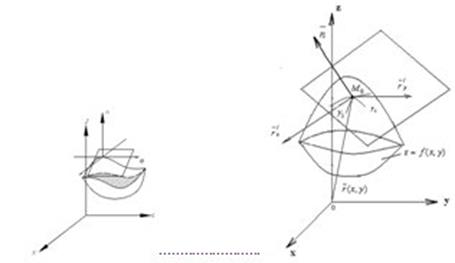
Поверхность будем рассматривать
1. как образ замкнутой области 
при непрерывном отображении
2. Отображение можно задать в векторном виде 
в каждой точке гладкой поверхности
3. Для 
существует нормаль 
, перпендикулярный к касательным 
кривым 
в точке 
. Следовательно равен векторному произведению касательных к векторов:
, 
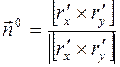
поверхность
-
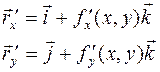направление касательных прямых к 
и 
в т.
к поверхности 
.
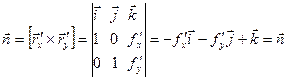
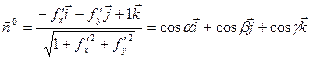Направляющие косинусы нормали 
к поверхности
Задание векторного поля характеризует задание вектор функции:
Примеры векторных полей:
- поле скоростей текущей жидкости или газа.
- гравитационное поле
- электростатистическое поле.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--