Реферат: Вычисление интеграла по поверхности

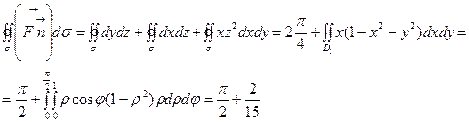
Пример 4.

Пример 5.

Теорема Остроградского-Гаусса.

Дивергенция.

-поток вектора через поверхность в направлении за единицу времени есть разность между количеством жидкости вытекающей из области и количеством жидкости втекающей в область .

1. . Следовательно из области жидкости вытекает столько же сколько втекает.

2. жидкости или газа вытекает больше, внутри существует источник .

3. жидкости или газа втекает больше чем вытекает , внутри существует сток.

Чтобы оценить мощность источников и стоков внутри нам необходима теорема Остроградского-Гаусса.

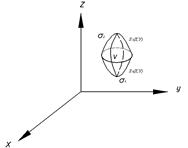
Если -непрерывна вместе с частными производными в области то:

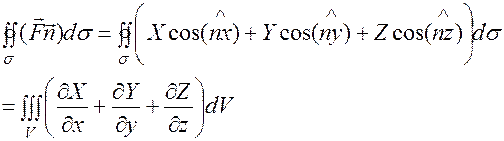
Поток изнутри равен суммарной мощности источников и стоков в области

за единицу времени.

Величина потока вектора через замкнутую поверхность :

является глобальной характеристикой векторного поля в области и очень приблизительно позволяет судить о наличии источников и стоков в области .

· Поток представляет собой избыток жидкости протекающей в сторону положительной нормали , а не абсолютное количество жидкости прошедшей через независимо от направления течения. В связи с этим удобно ввести локальную характеристику распределения стоков и источников. Такой характеристикой является дивергенция (плотность потока в точке):

Дивергенция:

Определение: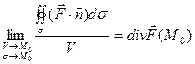- стягивается в точку.

Определение: Дивергенцией векторного поля в точке называется предел отношения потока векторного поля через поверхность к объему , ограниченному этой поверхностью, при условии что поверхность стягивается в точке .

Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля исходящего из точки , т.е. мощность источника и стока находящегося в точке .

- средняя объемная мощность потока .

-существует источник в точке .