Реферат: Вычисления площади произвольного многоугольника

angle: real;

end;

А количество вершин в глобальной переменной n.

Следующая процедура осуществляет ввод данных:

procedure input;

var f: text;

i: integer;

begin

Assign(f,'points.dat');

reset(f);

readln(f, n);

for i:=1 to n do readln(f, sd[i].x, sd[i].y);

end;

2) Предварительная обработка.

В данном пункте алгоритма осуществляется вычисление внутренних углов многоугольника.

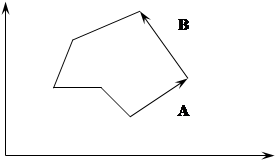Рассмотрим часть произвольного многоугольника:

Пусть вектор A образует с ось OX угол a₁ , а вектор B – угол a₂ . Тогда угол между ними (внутренний угол многоугольника) будет равен 180–a₁ –a₂ . Здесь нельзя использовать формулу угла между векторами через скалярное произведение, т.к таким образом вычисляется минимальный угол. Но при этом возможен такой случай:

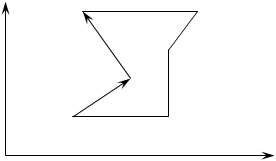Угол будет внешним.

Так вычислим либо все внутренние, либо все внешние углы многоугольника. Чтобы выяснить какие углы мы нашли, рассмотрим следующую теорему:

Сумма внешних углов произвольного многоугольника больше суммы внутренних.

Доказательство проведем по индукции:

1) Очевидно, что теорема справедлива для треугольника

2) Предположим, что теорема справедлива для k-угольника

3) Докажем теперь, что теорема справедлива для (k+1)-угольника.

Пусть сумма внутренних углов k-угольника равна a₁ , а внешних a₂ . Из п.2 следует, что a₁ <a₂ . k–угольник можно сделать (k+1)-угольником "нарастив" его на один треугольник:

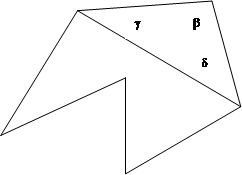Тогда сумма внутренних узлов (k+1)-угольника – a₁ +b+g+d, а внешних a₂ +(360-b)-g-d. Из геометрии известно, что сумма углов треугольника равна 180⁰ . Тогда:

сумма внутренних углов: a₁ +180

сумма внешних углов: a₂ +360-(b+g+d)=a₂ +180.

Но из п.2 следует, что a₁ <a₂ . Следовательно, сумма внешних углов (k+1)-угольника больше суммы внутренних.(k+1)-угольника.