Реферат: Вычисления площади произвольного многоугольника

Внутренние углы многоугольника будем вычислять следующим образом:

· для i-той вершины, имеющей координаты (X_i , Y_i ) найдем координаты входящих и выходящих векторов:

A {X_i –X_i–1 , Y_i –Y_i–1 } – входящий вектор

B {X_i+1 –X_i , Y_i+1 –Y_i } – выходящий вектор

· Вычисляем углы, образованные этими векторами с осями координат

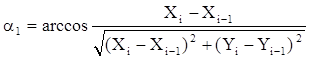
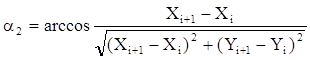
· Вычисляем угол i-той вершины j_i =180–a₁ –a_2.

· Находим сумму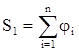

· Находим сумму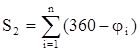

· Если S₁ <S₂ , то найденные углы являются внутренними, в противном случае внутренние углы равны 180-j_i .

В языке Turbo Pascal нет функции Arccos(x), поэтому его вычисляем, используя следующую формулу 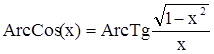. Но значение этой функции может изменяться в интервале от –90⁰ до 90⁰ , поэтому при вычислении действительного угла будем учитывать квадрант, в котором лежит вектор.

Если в процессе отсечения углов произойдет ситуация, что три вершины подряд окажутся на одной прямой, то необходимо вторую из них удалить, т.к. она, строго говоря, не является вершиной и не будет влиять на дальнейшие вычисления. Для определения, лежит ли i-ая вершина на прямой, соединяющей (i–1)-ую и (i+1)-вершины, аналогично найдем входящий и выходящий вектора A и B . Затем их нормируем, т.е. делим каждую координату вектора на модуль этого вектора. Если после этого вектора окажутся равны, т.е. окажутся равными их координаты, то i-тую вершину можно удалить.

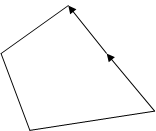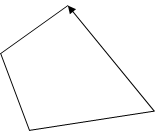Учитывая все вышеприведенное, составляем процедуру вычисления внутренних углов.

procedure Angles;

var

al1,al2,

dx, dy, dxp, dyp,

s_in, s_out, a: real;

i,j: integer;

function ArcCos(a: real): real;

var res: real;

begin

if abs(a)<1.0E-30 then res:=pi/2

else res:=ArcTan(sqrt(1-a*a)/a);

if dx<0 then

if dy>=0 then res:=pi+res

else res:=-pi-res

else