Реферат: Вычисления площади произвольного многоугольника

dy:=sd[i+1].y-sd[i].y;

al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));

sd[i].angle:=pi-al1+al2;

if sd[i].angle>2*pi then sd[i].angle:=sd[i].angle-2*pi

else

if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;

al1:=al2

end;

dx:=sd[1].x-sd[n].x;

dy:=sd[1].y-sd[n].y;

al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));

sd[n].angle:=pi-al1+al2;

if sd[n].angle>2*pi then sd[n].angle:=sd[n].angle-2*pi

else

if sd[n].angle<0 then sd[n].angle:=2*pi+sd[n].angle;

s_in:=0;

s_out:=0;

for i:=1 to n do

begin

if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;

S_in:=S_in+sd[i].angle;

S_out:=S_out+(2*pi-sd[i].angle);

end;

if S_out<S_in then

for i:=1 to n do sd[i].angle:=2*pi-sd[i].angle;

end;

3) Нахождение выпуклых вершин.

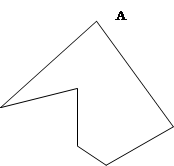
Как было сказано выше, внутренний угол выпуклой вершины меньше 180⁰ . Но не всякую выпуклую вершину можно "отрезать", т.к. линия "отреза" может пересекать стороны многоугольника. Например, вершину А "отрезать" нельзя:

Эта задача сводится к задаче о пересечении двух отрезков. Пусть отрезки заданы координатами своих концов. Первый отрезок A₁ (X_1A , Y_1A ) и