Реферат: Зависимость между деформациями и напряжениями при плоском и объемном напряженных состояниях

В следующем параграфе показывается применение этого принципа к расчету простейших статически-неопределимых систем.

О других свойствах механической энергии будет сказано далее, в соответствующих местах курса.

СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ

Имеется много конструкций, в элементах которых усилия не могут быть определены только из уравнений равновесия.

Такие конструкции (системы) называются статически неопределимыми.

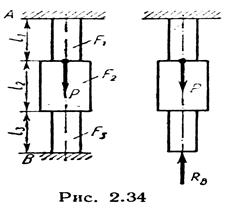
Рассмотрим, например, стержень, изображенный на рис. 4. Нагрузка Р воспринимается частично верхней заделкой и частично нижней. Для определения двух реакций, возникающих в заделках, можно использовать только одно уравнение равновесия: равенство нулю суммы проекций всех сил на вертикальную ось. Остальные два уравнения равновесия обращаются в тождества.

Поскольку неизвестных — два, а уравнение равновесия — одно, то потребуется составить одно рис 4 дополнительное уравнение, рассматривая деформации стержня или перемещения его сечений. Такие системы называются системами один раз (однажды) статически неопределимыми.

Системы, требующие составления двух уравнений перемещений, называются дважды статически неопределимыми и т. д.

Для решения рассматриваемой задачи поступим следующим образом.

Отбросим одну заделку, например нижнюю, заменив ее действие на стержень неизвестной реакцией.

В полученной таким образом системе (обычно ее называют основной системой) приравняем нулю перемещение нижнего сечения, так как в заданной системе это сечение заделано и перемещаться не может.

От действия силы Rbсечение В будет перемещаться вверх в результате укорочения всего стержня, а от действия силы Р — вниз в результате удлинения верхней части стержня длиной 1_Ъ так как сила Р при отброшенной нижней заделке передается на верхнюю заделку только через эту часть стержня.

Для определения деформаций используем закон Гука. Так как площадь сечения стержня разная на различных участках, то деформацию определяем по частям.

Уравнение перемещений имеет вид

Первые три члена представляют собой перемещение вверх сечения В под действием силы R_B , четвертый член — перемещение вниз сечения В от действия силы Р. Из этого уравнения находим R_B , после чего определение продольных сил в сечениях производится без затруднений по методу сечений, как показано в предыдущих параграфах.

Литература

1 Феодосьев В.И. Сопротивление материалов. 2002

2 Беляев Н.М. Сопротивление материалов. 1999

3 Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем. 1991

4 Работнов Ю.Н. Механика деформируемого твердого тела. 2004

5 Степин П.А. Сопротивление материалов. 1990