Реферат: Знакомство со средой MS Excel

a₁₁ x₁ +a₁₂ x₂ +··· + a_1n x_n =b₁ ,

a₂₁ x₁ +a₂₂ x₂ +··· + a_2n x_n =b₂ ,

a_n1 x₁ +a_n2 x₂ +··· + a_nn x_n =b_n .

Эту систему можно представить в матричном виде

АХ=b,

где- матрица коэффициентов системы уравнений;

-вектор правых частей

-вектор неизвестных

При выполнении лабораторной работы СЛАУ необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.

Метод обратной матрицы.

Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:

А^-1 Ах=А^-1 b,

Ex=A^-1 b, (E единичная матрица)

Таким образом, вектор неизвестных вычисляется по формуле x=A^-1 b.

Метод Крамера.

В этом случае неизвестные x₁ ,x₂ ,… , x_n вычисляются по формуле:

где ∆ - определитель матрицы A, ∆i - определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.

Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, где будет храниться результат, и после получения результата необходимо преобразовать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.

Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на примере следующей системы

В этом случае матрица коэффициентов А и вектор свободных членов b имеют вид

Введём матрицу A и вектор b в рабочий лист MS Excel (см. рис. 21)

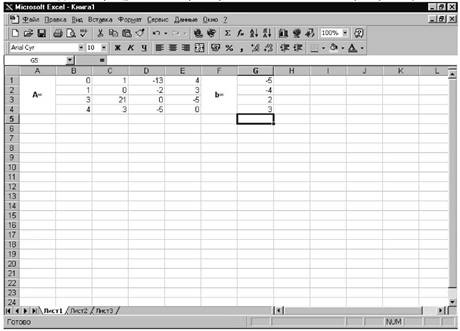
Рисунок 21