Шпаргалка: 5 различных задач по программированию
Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (5), для получения которого достаточно было принять в системе (5) неизвестную х1 за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять второе, так как
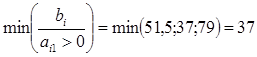 , а разрешающим элементом будет а21 =4.
, а разрешающим элементом будет а21 =4.
Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.
| 36 32 10 13 0 0 0 | ||||
| Базис | Н | x1 x2 x3 x4 x5 x6 x7 | Пояснения | ||
| 0 | Х5 | 103 | 2 3 4 1 1 0 0 | z0 = | |
| 0 | Х6 | 148 | 4 2 0 2 0 1 0 | ||
| 0 | Х7 | 158 | 2 8 7 0 0 0 1 | ||
| z0 -z | 0 - z | -36 -32 -10 -13 0 0 0 | |||
| 0 | Х5 | 29 | 0 2 4 0 1 -1/2 0 | ||
| 0 | Х1 | 37 | 1 1/2 0 1/2 0 ј 0 | ||
| 36 | Х7 | 84 | 0 7 7 -1 0 -1/2 1 | min (29/2; 64;12)=12 | |
| z0 -z | 1332-z | 0 -14 -10 5 0 9 0 | min (-14;-10) = -14 | ||
| 36 | Х5 | 5 | 0 0 2 2/7 1 -5/14 -2/7 | ||
| 0 | Х1 | 31 | 1 0 -1/2 4/7 0 2/7 -1/14 | ||
| 14 | Х2 | 12 | 0 1 1 -1/7 0 -1/14 1/7 | ||
| z0 -z | 1500-z | 0 0 4 3 0 8 2 | все Dj ³0 |
Применим известные формулы исключения
a`ij =aij – (ais /ars )*arj
a`iq =aiq – (ais /ars )*arq
b`i =bi - (ais /ars )*br
b`r =br /ars
s=1, r=2
a`12 =3-2/4 *2= 2
a`13 =4
a`14 =1-2/4 *2=0
a`15 =1
a`16 =0-2/4*1= -2/4
a`17 =0
a`32 =8-2/4* 2= 7
a`33 =7
a`34 =0-2/4* 2= -1
a`35 = 0
a`36 =0-2/4 *1= -2/4
a`37 =1
a`21 =a21 /a21 =1
a`22 =a22 /a21 =1/2
a`23 =0
a`24 =1/2
a`25 =0
a`26 =1/4
a`27 =0
a`41 = 0