Эта система преобразуется к виду

2 x₃ + 2/7 x₄ + x₅ – 5/14 x₆ – 2/7 x₇ = 5

x₁ - Ѕ x₃ + x₄ + 2/7 x₆ – 1/14 x₇ = 31 (18)

x₂ + x₃ - 1/7 x₄ – 1/14 x₆ + 1/7 x₇ = 12

4 x₃ + 3 x₄ + 8 x₆ + 2 x₇ = 1500 - z

Первые три уравнения системы (18) представляют некоторый предпочитаемый эквивалент системы уравнений (5) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи

x₁ =37, x₂ =0, x₃ =0, x₄ =0, x₅ =29, x₆ =0, x₇ =84 (19)

т.е. определяют производственную программу x₁ =37, x₂ =0, x₃ =0, x₄ =0 (20)

и остатки ресурсов:

первого вида х₅ =5

второго вида х₆ =0 (21)

третьего вида х₇ =0

Последнее уравнение системы (18) мы получаем, исключая х₂ . В последнем уравнении системы (18) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные

z = 1500 - 4 x₃ - 3 x₄ - 8 x₆ - 2x₇ (22)

то становится совершенно очевидным (в силу того, что все xj³0), что прибыль будет наибольшей тогда, когда

x₃ =0, x₄ =0, x₆ =0, x₇ =0 (23)

Это означает, что производственная программа (20) является наилучшей и обеспечивает предприятию наибольшую прибыль z_max = 1500 (24)

Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.

Следует обратить внимание на экономический смысл элементов последней строки последней симплексной таблицы. Например, коэффициент D₃ =4 при переменной х₃ показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 4 единиц.

Воспользуемся тем, что в оптимальной производственной программе x₃ =0, x₄ =0. Предположим, что четвертую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:

Следует при этом обратить внимание на то, что последовательное улучшение производственной программы (x₁ =0, x₂ =0) ® (x₁ =37, x₂ =0) ® (x₁ =31, x₂ =12) на графике означает движение от одной вершины многогранника допустимых решений к другой вершине по связывающей их стороне многоугольника.

ДВОЙСТВЕННАЯ ЗАДАЧА

Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.

Теперь представим себе, что знакомый предприниматель П, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у₁ рублей за каждую единицу первого ресурса, у₂ руб – второго, у₃ руб – третьего. Возникает вопрос: при каких ценах у₁ , у₂ , у₃ мы можем согласиться с предложением П.

Величины у₁ , у₂ , у₃ принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.

Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид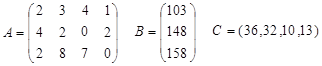

Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 4 единицы ресурса второго вида и 2 единицы третьего (элементы первого столбца матрицы). В ценах у₁ , у₂ , у₃ наши затраты составят 2у₁ + 4у₂ + 2у₃ , т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы продукции первого вида. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше 2у₁ + 4у₂ + 2у₃ ³ 36.

Аналогично, для трех оставшихся видов продукции:

3у₁ + 2у₂ + 8у₃ ³32

4у₁ + 7у₃ ³10