Шпаргалка: 5 различных задач по программированию

a`₄₃ = -10

a`₄₄ =5

a`₄₅ =0

a`₄₆ =9

a`₄₇ =0

a`<sub>11</sub> =a`₃₁ =0

b`₁ =103-148/4*2=29

b`₂ =148/4=37

b`₃ =158-148/4*2=84

Получаем для системы уравнений (5) новый предпочитаемый эквивалент

2x₂ + 4x₃ + x₅ - 1/2x₆ = 29

x₁ + 1/2x₂ + 1/2x₄ + 1/4x₆ = 37 (11)

7x₂ + 7x₃ - x₄ -1/2x₆ + x₇ = 84

Приравняв к нулю свободные переменные х₂ , х₃ , х₄ , х₆ , получаем базисное неотрицательное решение, совпадающее с (10), причем первые четыре компоненты его определяют новую производственную программу х₁ =37, х₂ =0, х₃ =0, х₄ =0. (12)

Представим соотношение (2) в виде уравнения -36х₁ - 14х₂ - 10х₃ - 13х₄ = 0 – z (13)

и припишем его к системе (5). Получается вспомогательная система уравнений

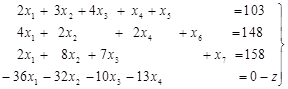(14)

Напомним, что разрешающую неизвестную в системе (5) мы выбрали х₁ . Этой переменной в последнем уравнении системы (14) отвечает наименьший отрицательный коэффициент D₁ = -36. Затем мы нашли разрешающий элемент а₂₁ =4 и исключили неизвестную х₁ из всех уравнений системы (5), кроме второго. Далее нам пришлось х₁ исключать и из функции (2). Теперь это можно сделать очень просто, если посмотреть на систему уравнений (14). Очевидно, достаточно умножить второе уравнение системы (14) на 9 и прибавить к четвертому; получим

-14х₂ - 10х₃ + 5х₄ - 9х₆ = 1332 – z (15)

Таким образом, мы преобразовывали вспомогательную систему уравнений (14) к виду

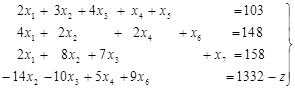(16)

Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент (11) системы уравнений (5) и определяют базисное неотрицательное решение (10) и производственную программу (12), а из последнего уравнения системы (16) получается выражение функции цели через свободные переменные. Получим следующий предпочитаемый эквивалент системы условий, который определит для системы (5) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого нам придется выразить функцию z=1332+14x₂ +10x₃ -5x₄ -9x₆ через новые свободные переменные, удалив оттуда переменную х₂ , ставшую базисной.

Очевидно, если имеется хотя бы один отрицательный коэффициент Dj при какой-нибудь переменной x_j в последнем уравнении системы (16), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. Мы нашли в последнем уравнении системы (16) наименьший отрицательный коэффициент min(Dj<0) = min(-14,-10) = -14 = D_2. Поэтому принимаем х₂ в системе (11) за разрешающую неизвестную, находим разрешающее уравнение по (17)

и исключаем х₂ из всех уравнений системы (11), кроме третьего уравнения. Укажем разрешающий элемент а₃₂ =7.

Теперь мы будем преобразовывать вспомогательную систему (16), по формулам исключения.

a`_ij =a_ij – (a_is /a_rs )*a_rj

a`_iq =a_iq – (a_is /a_rs )*a_rq

b`_i =b_i - (a_is /a_rs )*b_r

b`_r =b_r /a_rs