Шпаргалка: Шпаргалка по Статистике 3

Функция распределения.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытаний примет значения, меньше х, т.е. F(x)=P(X<x). Эта функция существует как для непрерывных, так и для дискретных величин.

Плотность вероятности.

Плотность вероятности случайной величины X, функция р(х), такая, что при любых a и b вероятность неравенства а < Х < b равна .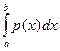

Их связь и свойства

Функция распределения вероятности — просто функция плотности вероятности, проинтегрированная от - до определенного значения. Для целочисленных случайных величин интеграл заменен суммированием по соответствующим индексам.

Функция распределения, свойства: 1. Значения функции распределения принадлежат отрезку (0,1): ; 2. F(x) - неубывающая функция, т.е. , если ; 3. Если возможные значения случайной величины принадлежат интервалу (a,b), то: 1) F(x)=0 при ; 2) F(x)=1 при ;

Плотность вероятности, свойства: 1) ; 2) 3) 4)

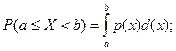
Автокорреляционная функция (АКФ)

Показывает связь сигнала (функции) с копией самого себя, смещённого на величину m.

График автокорреляционной функции можно получить, отложив по оси ординат коэффициент корреляции двух функций (базовой и функции сдвинутой на величину m) а по оси абсцисс величину m. Если исходная функция строго периодическая, то на графике АКФ тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности базовой функции, а следовательно и о её частотных характеристиках. Определяется выражением 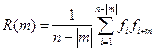, где значение поля в i-той точке. i=1…n. m – интервал принимающий значения . Свойства автокорреляционной функции: 1) АКФ – четная. Т.е. R(m)=R(-m). 2) При m=0, АКФ=D(дисперсии) 3) При сложении неслучайной функции φ(t) и случайного процесса АКФ процесса не меняется.4)При умножении случайного процесса на неслучайную функцию φ(t) АКФ процесса умножается на произведение φ(t_i ) φ(t_j ).

Вариант 4

Числовые характеристики положения случайной величины.

Такая характеристика случайной величины, как математическое ожидание, квантиль называется иногда характеристикой положения, так как она дает представление о положении случайной величины на числовой оси. Другими характеристиками положения являются мода и медиана.

y - квантиль — числовая характеристика закона распределения случайной величины; такое число, что данная случайная величина попадает левее его с вероятностью, не превосходящей: y

Модой М дискретной случайной величины называется ее наиболее вероятное значение, модой М непрерывной случайной величины – значение, в котором плотность вероятности максимальна.

Медиана Ме – делит вариационный ряд на две части, равные по числу вариантов. Если число вариантов нечётно, т.е. n=2k+1, то Me=, при четном n=2k, то Me=

Математическое ожидание MX (среднее значение) или сумма произведения всех её возможных значений на их вероятность.

Взаимно корреляционная функция (ВКФ)

ВКФ представляет собой оценку корреляционных свойств двух случайных процессов. Для эргодических случайных процессов ВКФ вычисляется по данным отдельных реализаций и . ВКФ по формуле где значение поля в i-той точке. i=1…n. m – интервал принимающий значения . n – число точек для каждой реализации. Допустим, что по реализации найдены их средние значения: и , тогда модно считать что , тогда получаем

Свойства взаимной корреляционной функции (ВКФ):

1) ВКФ не является ни чётной ни нечётной функцией, т.е. Rху(τ) не равно Rху(-τ).

2) ВКФ остаётся неизменной при перемене чередования функций и изменений знака аргумента, т.е. Rху(τ)=Rху(-τ). 3) Если случайные функции x(t) и y(t) не содержат постоянных составляющих и создаются независимыми источниками, то для них R_ху (τ) → 0. Такие функции называются некоррелированными.

Вариант 5

Числовые характеристики рассеяния случайной величины.

Числовые характеристики рассеяния случайных величин: дисперсия, среднее квадратическое от-клонение, коэффициент вариации.

Вводят числовую характеристику, которая называется дисперсией. Эта характеристика оценивает рассеяние случайной величины вокруг своего математического ожидания.

Дисперсия . D(C)=0, где С=соnst.

D(CX)=C*C*D(X).