Шпаргалка: Шпаргалка по Статистике 3

Основы выборочного метода изучения экспериментальных данных.

Суть этого метода: если по результатам изучения сравнительно небольшой ее части можно получить с достаточной для практики достоверностью необходимую информацию о всей совокупности, то нет необходимости в сплошном наблюдении. Часть объектов исследования, определенным образом избранная из более обширной совокупности, называется выборкой, а исходная совокупность, из которой взята выборка, — генеральной (основной) совокупностью. Число элементов в выборке называется объемом выборки (обозначается n).

Требование к выборке

Важным требованием к выборке является ее репрезентативность, то есть правильная представимость в ней пропорций генеральной совокупности. Достижению репрезентативности может способствовать такая организация эксперимента, при которой элементы выборки извлекаются из генеральной совокупности случайным образом. Обычно в статистике различают три типа значений переменных: количественные, номинальные и ранговые.

Первичный ряд

Рядом распределения в статистике называется упорядоченное распределение

единиц совокупности на группы по какому- либо варьирующему признаку.

Статистические данные представлены в рядах распределения. Статистические данные без какой-либо систематизации образуют первичный ряд.

Вариационный ряд

Вариационный ряд последовательность каких-либо чисел, расположенная в порядке возрастания их величин. Например, В. р. чисел 1, —3, 8, 2 имеет вид —3, 1, 2, 8. Промежуток между крайними членами В. р. называют интервалом варьирования, а длину этого интервала — размахом.

Формы представления статистических данных.

Существует 3 основных формы представления статистических данных: 1)Текстовая – включение данных в текст, применяется при малом количестве цифровых данных; 2)Табличная – представление данных в таблицах; 3)Графическая – выражение данных в виде графиков.

Гистограмма

Гистограмма - один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания в определенный (заранее заданный) интервал. Достоинства метода: 1)Наглядность, простота освоения и применения. 2)Управление с помощью фактов, а не мнений. 3)Позволяет лучше понять вариабельность, присущую процессу, глубже взглянуть на проблему и облегчить нахождение путей ее решения. Недостатки метода: Интерпретация гистограммы, построенная по малым выборкам, не позволяет сделать правильные выводы.

Ряд Фурье в комплексной форме.

Пусть функция f (x) определена в интервале [−π, π]. Применяя формулы Эйлера можно записать ряд Фурье данной функции в комплексной форме: 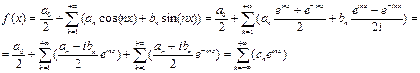,где,,. Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах.

Амплитудный и фазовый спектр

Комплексные коэффициенты ряда Фурье позволяют непосредственно выразить амплитуды гармоник и их начальные фазы. Амплитуда k-й гармоники равна и её начальная фаза

Распределение амплитуд гармонических составляющих сигнала в зависимости от частоты (номера гармоники) называется амплитудным спектром , распределение фаз этих составляющих от частоты – фазовым спектром. Амплитудный и фазовый спектры периодического сигнала являются линейчатыми, дискретными, они состоят из отдельных «линий», соответствующих дискретным частотам: 0; f1;2f1;f2 и т.д. Значение амплитудного и фазового спектров рассчитываются относительно принятого начала отчёта.

Вариант 11

Функция Лапласа

Производится nиспытаний, где вероятность появления А постоянна и равна p(0<p<1). Вероятность P_n (k₁ ,k₂ )-вероятность того что событие Aпоявится в n испытаниях от k₁ до k₂ . По теореме Лапласа: 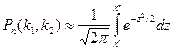, где , При решении задач, требующих применение теоремы Лапласа, пользуются специальными таблицами, так как 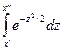не выражается через элементарные функции. 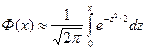Для удобства делаем . Ф(x)-функция Лапласа.

Вероятность попадания в интервал числовой оси для нормально распределенной случайной величины.

Функция распределения где и - параметры распределения. При =0 и =1 получаем , . Причём Ф(-х)=1- Ф(х). Ф(0)=0,5. Ф(-1)=-0,1587. Ф(1)=0,8413. Для нормального распределения почти всё отклонение от среднего , укладывается в интервале . Формула попадания случайной величины на заданный интервал (x1,x2). . Вероятности попадания случайной величины в интервалах ,,: P1=; P2=; P3=

«Правило трёх сигм»

Поскольку все значения случайной величины, а именно 99,7% укладывается в интервал 3σ, способ оценки диапазона возможных значений называется «правило трёх сигм». Из этого правила следует приближенный способ определения:

Дискретные преобразования Фурье

Формулы интегральных преобразований Фурье непрерывных функций преобразуются для дискретных данных в формулы, включающие суммы. Такие преобразования называются дискретными преобразованиями Фурье (ДПФ).

Прямое дискретное преобразование Фурье, которое позволяет получать дискретный спектр Х(k) по дискретному сигналу x(i), может быть выполнено по формуле где k-номер гармоники(дискретной частоты в спектре), i-номер точки в исходном сигнале, δT – шаг дискретизации исходного сигнала, N – количество точек в исходном сигнале.