Шпаргалка: Шпаргалка по Статистике 3

Плотность распределения

Функция распределения где и - параметры распределения. , При =0 и =1 получаем , . Причём Ф(-х)=1-Ф(х). Для нормального распределения почти всё отклонение от среднего , укладывается в интервале . Формула попадания случайной величины на заданный интервал (x1,x2). . Вероятности попадания случайной величины в интервалах ,,: P1=

P2=

P3=

Способ оценки диапазона возможных значений называется «правило трёх сигм». Асимметрия и эксцесс нормального закона равны нулю.

Ряд Фурье в полярных координатах

Амплитудный и фазовый спектр

Для тригонометрической формы ряда Фурье вводится амплитуда и фаза m-ой гармоники, связанные с коэффициентами Фурье соотношениями: ,

Тригонометрическая форма ряда Фурье:

Распределение амплитуд гармонических составляющих сигнала в зависимости от частоты (номера гармоники) называется амплитудным спектром , распределение фаз этих составляющих от частоты – фазовым спектром. Амплитудный и фазовый спектры периодического сигнала являются линейчатыми, дискретными, они состоят из отдельных «линий», соответствующих дискретным частотам: 0; f1;2f1;f2 и т.д. Значение амплитудного и фазового спектров рассчитываются относительно принятого начала отчёта.

Вариант 9

Равномерный закон распределения случайной величины.

Cплотностью

и функцией распределения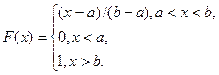

Среднее значение и дисперсия случайной величины, распределённой по равномерному закону, равны соответственно MX=(a+b)/2 и DX=(b-a)² /12.

Вероятность попадания случайной величины в интервал (x1,x2): P(x1<X<x2)=(x2-x1)/(a-b)

Асимметрия, ввиду симметрии плотности, равна нулю, а эксцесс равен – 1,2;

Биноминальный закон

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) =1-р = q.

Вероятность того, что при n испытаниях событие А наступит m раз: ;

- число сочетаний появления события А. М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях; D(m)=npq - дисперсия частоты появления события А;

Закон Пуассона

Принимает последовательно значения X=0,1,2,…,m… с вероятностью и дискретной функции распределения

Для закона Пуассона =D=a, a – параметр распределения. Закон Пуассона ассиметричен и его асимметрия A=, а эксцесс E=1/a, т.е. распределение право асимметрично и имеет положительный эксцесс.

Метод наименьших квадратов.

f(x) эта некая функция, конкретный вид которой не известен, известен лишь ее общий вид. МНК позволяет зная общий вид функции найти ее конкретный вид (коэффициенты) который наилучшим образом вписывается в экспериментальные данные. Основная идея МНК состоит в том, чтобы при нахождении конкретного вида функции минимизировать сумму квадратов ошибок во всех исходных уравнениях. Иными словами нужно свести к минимуму функцию:

Выравнивание

Выравнивание – замена нелинейной зависимости линейного вида и в обратном пересчёте параметров линейной регрессии. Таким образом, метод выравнивания заключается в следующем: предполагая, что между x и y существует зависимость определенного вида, находят некоторые величины и , которые при сделанном предположении оказываются связаны линейной зависимостью. Затем для заданных значений ивычисляют соответственные значенияии зображают их графически. Из графика легко увидеть, близка ли зависимость междуик линейной и, следовательно, подходит ли выбранная формула или нет.(→lny=lna+bx→Y=Ax+B)