Шпаргалка: Шпаргалка по Статистике 3

Вариант 12

Связь между коэффициентом корреляции и коэффициентами уравнения линейной регрессии

Связь

Явление подмен частот

При дискретизации с частотой Fd<2F_N невозможно отличить частоты больше частоты Найквиста F_N от частот главного диапазона (0- F_N ).Поэтому, если в изучаемом сигнале имеются составляющие частоты выше F_N , to их энергия будет отражена в главный диапазон спектра симметрично относительно F_N . Это объясняет необходимость максимального подавления в анализируемом сигнале частот выше частоты Найквиста.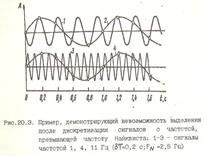

Частота Найквиста

Важной особенностью дискретного преобразования Фурье является наличие граничной частоты в дискретном спектре. Если ненулевые значения ординат спектра выходят за пределы этой границы по частоте, то невозможно точное восстановление по спектру функции x(t). Такой наивысшей из частот спектра является частота F_N = 1/(2δT) = Fd/2. Эта частота соответствует периоду, равному двум шагам дискретизации. Она играет важную роль в понимании результатов применения преобразований Фурье к дискретным данным и носит название частоты Найквиста. Частота Найквиста соответствует точке спектра Х(k) с номером k= целая чаcть [N/2]. ИЛИ

Исходный сигнал в результате разложения представляется суммой синусоидальных и косинусоидальных функций вида и , частоты которых кратны основной частоте , иначе они называются гармониками основной частоты , их периоды , а амплитуды и . Наивысшей из частот является частота Эта частота соответствует периоду, равному двум интервалам отсчёта, и называется частотой Найквиста .

Вариант 13

Интервальные оценки, их свойства.

Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Т, получила название методов интервального оценивания.

Способы построения интервальных оценок на примере оценки математического ожидания

Прямое и обратное интегральное преобразования Фурье.

Для непериодических функций следует естественным образом полагать, что период их бесконечно велик (Т→∞). При этом последовательность частот гармоник становится непрерывной и мы получаем интеграл Тут обединены два интегральных преобразования Фурье: прямое , обратное ; Заметим, что для непериодической функции спектр является непрерывным (сплошным).

Функция X(f) называется Фурье-образом функции x(t), а функция x(t) - оригиналом. Преобразования Фурье позволяют выполнять переход из временной области в частотную: от оригинала к образу (прямое преобразование Фурье) и обратно от спектра к временному представлению (обратное преобразование Фурье). Фурье-образ X(f) изучаемой непериодической функции x(t) является комплексной величиной.