Статья: Иррациональные уравнения и неравенства

3) Если 0<n<1, то

4) Если n³1, то

Ответ: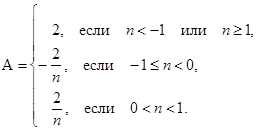

II. Иррациональные уравнения.

Рассмотрим уравнение вида .

Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть посторонние корни. Поэтому в уравнениях необходимо делать проверку.

Если уравнение содержит два и больше корней, то один из корней «уединяется», то есть уравнение приводится к виду .

Еще один способ решения – введение вспомогательной переменной.

Пример 3. Решить уравнения:

а) ;

б) ;

в) ;

г) .

Решение:

а) Û;

Проверка.

Þ х=-4 – посторонний корень,

– верно Þ х=2 – корень.

Ответ: х=2.

б)