Статья: Иррациональные уравнения и неравенства
![]()
Проверка.
![]()
![]() – это выражение не существует, т.е.
– это выражение не существует, т.е.
![]() – посторонний корень,
– посторонний корень,
![]()
![]() – верно Þ
– верно Þ![]() – корень.
– корень.
Ответ: ![]() .
.
в) ![]()
Введем вспомогательную переменную ![]() Þ x2=t2–13
Þ x2=t2–13
t2-13-2t=22; t2-2t-35=0,
t1=7; t2=-5.
Сделаем обратную замену:
![]() Û х2+13=49 Û х2=36 Þ х=±6,
Û х2+13=49 Û х2=36 Þ х=±6,
![]() – не имеет решений.
– не имеет решений.
Ответ: х=±6.
г) ![]()
Сделаем замену переменной. Положим ![]() . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
![]() Û
Û![]() Û
Û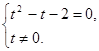
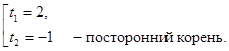
![]() Þ
Þ![]() Û
Û![]() Û
Û![]() Û
Û![]() .
.
Проверка показывает, что ![]() – корень.
– корень.
Ответ: ![]() .
.
III. Решение иррациональных неравенств.
При решении этих неравенств следует помнить, что в четную степень можно возводить неравенства с неотрицательными членами.
Поэтому неравенство ![]() эквивалентно системам
эквивалентно системам
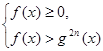 или
или ![]()
Неравенство ![]() равносильно системе
равносильно системе
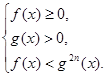
Пример 4. Решить неравенства:
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()