Статья: Локальная и нелокальная задачи для уравнения смешанного типа второго порядка с оператором Геллестедта
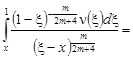
![]() , (8)
, (8)
где 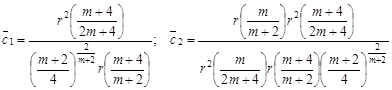 .
.
Обращая (8) как обобщенное интегральное уравнение Абеля относительно ![]() , получаем [2]:
, получаем [2]:
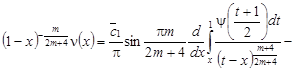
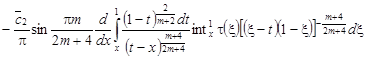 . (9)
. (9)
Или с учетом перестановки Дирихле порядка интегрирования во втором интеграле правой части (9), получаем:
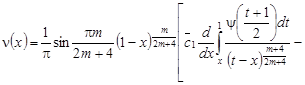
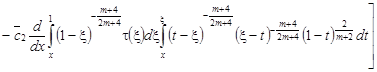 . (10)
. (10)
Рассмотрим
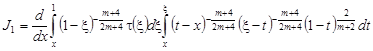 .
.
Произведя замену переменных ![]() в последнем равенстве, получим
в последнем равенстве, получим
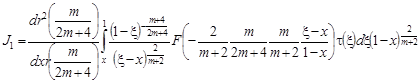 . На основании равенства [3]
. На основании равенства [3]
![]()
будем иметь
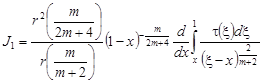 . (11)
. (11)
Подставляя (11) в (10), окончательно получаем функциональное соотношение между ![]() и
и ![]() , привнесенное из гиперболической части области Ω на линию y = 0:
, привнесенное из гиперболической части области Ω на линию y = 0:
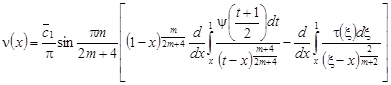 . (12)
. (12)
При m = 0 оно принимает вид:
![]() . (13)
. (13)
Устремляя ![]() из Ω1, получаем функциональное соотношение между
из Ω1, получаем функциональное соотношение между ![]() и
и ![]() , привносимое на линию y = 0 в виде:
, привносимое на линию y = 0 в виде:
![]() . (14)
. (14)
В начале рассмотрим случай, когда m = 0. Исключая из уравнения (13) и (14) ![]() и, учитывая краевые условия (2), приходим к задаче
и, учитывая краевые условия (2), приходим к задаче
![]() , (15)
, (15)
![]() . (16)
. (16)
Решение (15), (16) представим в виде:
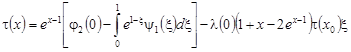 , (17)
, (17)
где обозначено
![]() .
.