Статья: Локальная и нелокальная задачи для уравнения смешанного типа второго порядка с оператором Геллестедта

После определения в области Ω1 приходим к задаче (1), (2) и . Нетрудно убедиться, что решение этой задачи удовлетворяет интегральному уравнению

, (18)

где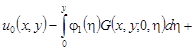

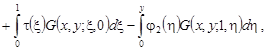
– функция Грина указанной выше смешанной задачи для уравнения теплопроводности. Отсюда, полагая в (18) x = x0, для функции получаем интегральное уравнение

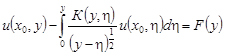(19)

с ядром

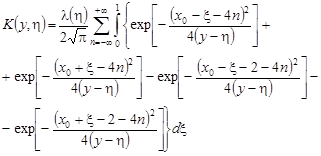
и правой частью .

Уравнение (19) является интегральным уравнением Вольтерра второго рода и оно безусловно разрешимо в пространстве .

ЗАДАЧА 2. Требуется найти функцию , удовлетворяющую всем условиям задачи 1, кроме второго условия из (2) и (4), вместо которых берут условия:

, (20)

. (21)

Для решения задачи 2, поступая как выше, с учетом условия (21) функцию однозначно определим решением уравнения (15), удовлетворяющим условиям

.

Пользуясь функцией Грина второй краевой задачи для уравнения теплопроводности, убеждаемся, что решение задачи 2 в области Ω1 удовлетворяет уравнению

, (22)

где .

Отсюда полагая в (22) x = x0 и учитывая условие (20), получаем систему интегральных уравнений Вольтерра второго рода относительно и :

(23)

,

,

,

.

В силу свойства функции Грина и ядер системы (23), нетрудно убедиться, что система уравнений (23) допускает единственное решение в пространстве [4].

Пусть теперь m > 0. Исключая из системы уравнений (12) и (15), получаем интегродифференциальное уравнение относительно :

, (24)