Статья: Локальная и нелокальная задачи для уравнения смешанного типа второго порядка с оператором Геллестедта

Доказана однозначная разрешимость локальной и нелокальной краевых задач для нагруженных уравнений 2 порядка оператора Геллестедта.

Рассмотрим уравнение

(1)

в области Ω, ограниченной отрезками АА0, ВВ0, А0В0 прямых соответственно и характеристиками

уравнения (1) в полуплоскости y<0, λ(y) – заданная непрерывная функция.

Пусть – параболическая, - гиперболическая области Ω, - интервал прямой y=0.

ЗАДАЧА 1. Найти в областях Ω1, Ω2 решение

уравнения (1), удовлетворяющее краевым условиям

, (2)

, (3)

где - непрерывные, а - дважды непрерывно дифференцируемая функции, причем

. (4)

Решение задачи Коши для уравнения (1), y<0, в области Ω2 имеет вид [1]:

, (5)

где .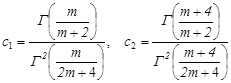

Удовлетворяя (5) заданному условию (3), получим

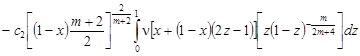. (6)

В равенстве (6) сделаем замену

.

В результате получим

.

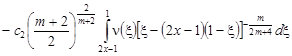Заменяя в последнем равенстве x через , получаем:

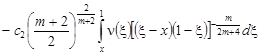. (7)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--