Статья: Метод изображений в электростатике

d-R

R-x

=

d+R

R+x

.

Отсюда x = R2/d.

Если мы поместим точечный заряд q на расстоянии х от центра сферы, то сфера будет эквипотенциальной поверхностью. Величина заряда q легко определится из соотношения

q = -

R-x d-R

q = -

R d

q.

Таким образом, имеем систему двух точечных зарядов, расположенных так, как на рис. 7.

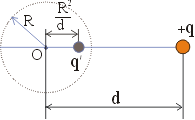
Рис. 7

На заряд +q со стороны сферы (или заряда-изображения q) действует сила притяжения

F = k

q|q| (d-x)2

= k

q2 d2-R2

.

Mы рассмотрели случай заземленной проводящей сферы. А как быть в том случае, если сфера имеет заряд Q или несет ненулевой потенциал? Ответ на этот вопрос очень прост - в центр сферы нужно добавить еще один точечный заряд q, величину которого определим из условия эквипотенциальности сферы.

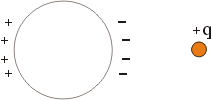
Рассмотрим незаряженную металлическую изолированную сферу и заряд +q, расположенный на расстоянии d от ее центра. Какая сила действует на заряд? Cфера останется незаряженной. Произойдет лишь перераспределение зарядов по поверхности сферы, связанное с взаимодействием с зарядом +q. Ближняя к заряду часть сферы приобретет отрицательный заряд, а дальняя - положительный, так как электроны притянутся к заряду (рис. 8).