Статья: Метод изображений в электростатике

q

r1

.

Если диэлектрическая проницаемость первой среды больше, чем второй, то заряд отталкивается от границы диэлектриков, при обратном соотношении - притягивается. Заряд, находившийся вначале в среде с большей проницаемостью, отталкиваясь от границы, стремится уйти в бесконечность. Заряд, вначале находившийся в среде с меньшей проницаемостью, притягивается к границе, пересекает ее, а затем, находясь уже в другой среде отталкивается от границы, стремясь уйти в бесконечность. Естественно, все сказанное справедливо только в том случае, если можно пренебречь силой трения, действующей на заряд со стороны среды.

И в заключение этой задачи поговорим о граничных условиях на границе раздела двух сред. Начнем с рассмотрения диэлектрических сред. Пусть мы имеем плоскую границу двух однородных диэлектриков с различными проницаемостями 1 и 2. Обозначим через

 E1

и

 E2

напряженности электрического поля в первой и во второй средах соответственно. Разложим векторы

 E1

и

 E2

на две составляющие - нормальную En1 и En2 и тангенциальную E1 и E2.

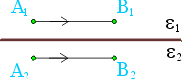
Рис. 14

Выясним теперь, как связаны тангенциальные составляющие поля при переходе из одной среды в другую. Выберем любые две пары точек, расположенных очень близко к друг к другу и разделенных поверхностью (рис. 14). Пара точек A1 и B1 находится в первом диэлектрике, а пара точек A2 и B2 находится во втором диэлектрике. Если тангенциальные составляющие полей в разных диэлектриках будут различными, то работы поля при перемещении какого-либо заряда вдоль линий A1B1 и A2B2 будут различными. Будем приближать точки A1 и A2, B1 и B2 друг к другу, в конце концов мы получим две бесконечно близких линии A1B1 и A2B2. Поскольку электрическое поле потенциально, то работа по перемещению заряда между какими-либо точками не зависит от траектории. У нас же получается, что работа поля по перенесению заряда по двум бесконечно близким отрезкам A1B1 и A2B2 различна. Следовательно наше допущение о неравенстве тангенциальных составляющих поля не верно, так как ведет к нарушению потенциальности поля.

Таким образом, на границе раздела двух диэлектриков тангенциальные составляющие поля в разных средах одинаковы или непрерывны, то есть E1 = E2.

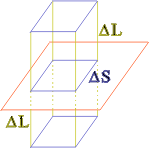
Рис. 15

Получим граничные условия для нормальных составляющих поля. Для этого выделим на поверхности прямоугольник S столь малый, что поля в диэлектриках с проницаемостями 1 и 2 на его площади не меняются. Построим на нем параллелепипед высоты 2L (рис. 15). Величина L должна быть достаточно малой, чтобы электрическое поле на протяжении отрезка L оставалось постоянным. Определим поток  поля через поверхность прямоугольного параллелепипеда. Потоки через боковые грани поверхности равны нулю, так как для них углы между напряженностью поля и нормалями (перпендикулярами) к поверхности равны 90. Таким образом остается только посчитать потоки через верхнюю и нижнюю грани параллелепипеда. Поскольку верхняя грань находится в среде с проницаемостью 1, а нижняя - в среде с проницаемостью 2, суммарный поток через них определится следующим образом

 = ниж+верх = 1 En1S-2 En2S.

С другой стороны, по теореме Гаусса имеем = 0, так как свободных зарядов внутри параллелепипеда нет. Следовательно, 1 En1 = 2 En2.

Если мы имеем две металлические среды, то тангенциальная составляющая поля на поверхности равна нулю (если бы она не была равна нулю, то электроны бы двигались против поля, а это означает, что точки на поверхности металла имеют разные потенциалы).

Точечный заряд и проводящие плоскости, образующие двугранный угол

Двугранный угол между двумя заземленными металлическими плоскостями равен . Внутри угла на расстоянии a и b от плоскостей находится точечный заряд +q. Найти электрическое поле внутри угла. Рассмотреть случаи: а)  = 90, б)  = 60, в)  = 45.