Статья: Разбиение чисел
Например, разбиение (5, 5, 5, 1, 1, 1, 1, 1, 1) соответствует разбиению (10, 5, 4, 2), поскольку число пятёрок равно 3 = 21 + 20, а число единиц равно 6 = 22 + 21.
Упражнения
3. Докажите, что в результате второго преобразования получается разбиение с различными частями.
4. Докажите, что если сначала выполнить преобразование Глэйшера, а затем обратное, то получится исходное разбиение.
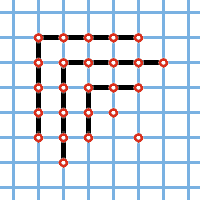
Существует другое, не менее интересное и совершенно неожиданное доказательство теоремы Эйлера, принадлежащее американскому математику XIX века Дж. Сильвестру. Вот конструкция Сильвестра: пусть имеется разбиение числа n на нечётные части: (2k1+1, 2k2+1, ..., (2kq+1), где k1 ≥ k2 ≥ ... ≥ kq. На листе клетчатой бумаги в некотором её узле поставим точку x1. Справа от x1, поставим в узлах k1 точек и столько же точек поставим в узлах, расположенных под точкой x1. Затем проделаем то же самое с числом k2, взяв в качестве исходной точку x2, расположенную в следующем за точкой x1 по диагонали направо вниз узле, и т.д., пока не дойдём до числа kq.
Например, разбиению на нечётные части (9, 9, 5, 1, 1) числа 25 будет отвечать картинка, изображённая на рис. 1.
|
Рис. 1. |
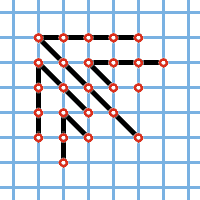
Рис. 2. |
Она состоит из симметричных относительно диагонали уголков, так что в самом верхнем уголке 2k1+1 точек, в следующем 2k2+1 точек и т.д., а всего точек будет n. Теперь проведём на той же картинке линии так, как показано на рис. 2, подсчитаем количество точек на каждой из этих линий и образуем из полученных таким образом чисел разбиение. Оказывается, все части этого разбиения различны.
Упражнение 5. Докажите это утверждение.
В нашем примере получится разбиение (9, 6, 5, 4, 1). Подумайте, как построить по разбиению на различные части разбиение на нечётные, т.е. восстановить по такому разбиению исходную симметричную картинку.
Отступление: решение задачи М1065
В этом разделе используется более сложная техника, чем в остальной части статьи. При желании вы можете пробежать его, не вникая в детали, и продолжить чтение со следующего раздела. Итак, займёмся решением задачи М1065 из «Задачника «Кванта» (1987, № 9). Напомним её формулировку.
Будем рассматривать векторы (x, y) с целыми неотрицательными координатами, причём хотя бы одна из координат отлична от 0. Назовём такой вектор образующим, если |x–y| = 1.
а) Докажите, что рассматриваемый вектор (x, y) можно представить в виде суммы различных образующих (или он сам — образующий) тогда и только тогда, когда величина k(x, y) = x + y – (x–y)2 неотрицательна.
б) Докажите, что число N(x, y) различных (с точностью до порядка) представлений вектора (x, y) в виде суммы различных образующих зависит только от числа k = k(x, y). Найдите N(13, 18).
Решение задачи начнём с того, что найдём общий вид целочисленных решений неравенства k(x, y) ≥ 0. Числа x+y и x–y имеют одинаковую чётность, поэтому k(x, y) является чётным при любых целых x, y. Следовательно, для любого целого m≥0 достаточно найти целочисленные решения уравнения x + y – (x–y)2 = 2m. Положим x–y = q. Тогда x+y = 2m+q2. Из этих двух равенств немедленно получаем:
| (3) |
где q — любое целое число, а m ≥ 0.
Смысл чисел m и q станет более наглядным, если представлять себе векторы вида (3) при m=0 как точки с целыми координатами параболы k(x, y) = 0, лежащей в плоскости (x, y). (Вы понимаете, почему это парабола?) Тогда полученные нами целочисленные решения неравенства k(x, y) ≥ 0. показывают, что все точки с целыми координатами, лежащие на параболе k(x, y) = 0 и внутри неё, получаются сдвигами целых точек этой параболы на векторы (m, m) (рис. 3). Удобно считать, что число m (m=0, 1, 2, ...) — номер параболы, на которой лежит точка (x, y), a q = x–y = 0, ±1, ±2, ... — номер точки на этой параболе.
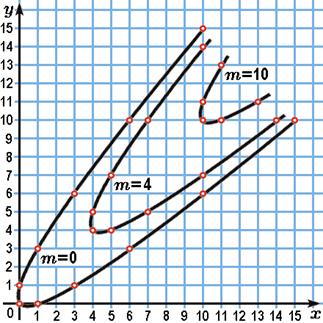
Рис. 3.
Поскольку условия задачи симметричны относительно перестановки координат векторов, достаточно доказать все утверждения для таких векторов (x, y), что x ≥ y, т.е. для векторов вида (3) с q ≥ 0.
Докажем достаточность условия в пункте а) задачи. По формуле суммы арифметической прогрессии
| 1 + 2 + ... + (q–1) + m + q = m + |
К-во Просмотров: 546
Бесплатно скачать Статья: Разбиение чисел
|