Статья: Целая и дробная части действительного числа

Решение

1). ООФ: х R

2). МЗФ: y Z

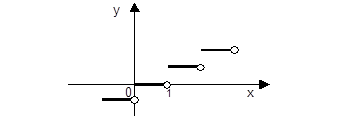
3). Т.к. при х О [ m ; m + 1), где m О Z , [ x ] = m, то и y = m, т.е. график представляет совокупность бесконечного множества горизонтальных отрезков, из которых исключены их правые концы. Например, х О [ -1 ; 0 ) Ю [ x ] = -1 Ю y = - 1 ; x О [ 0; 1) Ю [ x ] = 0 Ю y = 0.

Примечание.

1. Имеем пример функции, которая задается разными аналитическими выражениями на разных участках.

2. Кружочками отмечены точки, не принадлежащие графику.

Определение 2.

Дробной частью действительного числа х называется разность х – [ x ]. Дробная часть числа х обозначается символом { x }.

Пример.

Вычислить { x }, если х принимает значение : 2,37 ; -4 ; 3,14 . . .; 5 .

Решение

{ 2,37 } = 0,37 , т.к. { 2,37 } = 2,37- [ 2,37 ] = 2,37 – 2 = 0,37.

, т.к.

{ 3,14…} = 0,14… , т.к. { 3,14…} = 3,14…-[ 3,14…] = 3,14…-3= 0,14…

{ 5 } = 0 , т.к. { 5 } = 5 – [ 5 ] = 5 – 5 = 0.

Свойства дробной части действительного числа.

1°. { x } = x – [ x ]

2°. 0 { x } < 1

3°. { x + m } = { x }, где m О Z

4°. { x } = x , если х О [ 0 ; 1)

5° Если { x } = а , a О [ 0 ; 1), то х =а +m, где m О Z

6°. { x } = 0 , если х О Z.

Рассмотрим примеры применения понятия { x } в различных упражнениях.

Пример 1.

Решить уравнения:

1.1 { x } = 0,1

1.2 { x } = -0,7