Статья: Вычисление собственных чисел и собственных функций опрератора Штурма-Лиувилля на полуоси

, (2.1)

, (2.2)

где монотонно, т.е. уравнение (2.1) имеет не более одной точки поворота. Таким образом, для любого . В случае, когда , спектральная задача имеет дискретный спектр. Из представленного метода решения регулярной задачи следует, что ; таким образом, для каждого задачи на полуоси ставится в соответствие своя регулярная задача на конечном отрезке . Если бы мы знали все значения собственных функций , соответствующие собственным числам задачи на полуоси, в точке , то, решая задачи на конечном промежутке с дополнительным граничным условием , мы могли бы вычислить все собственные числа задачи на достаточно точно. Исходя из сказанного, можно утверждать, что погрешность определения собственных чисел тем меньше, чем точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых условия (условие Дирихле) и (условие Неймана). Пусть - собственные числа задач на конечном промежутке с дополнительными условиями Дирихле и Неймана соответственно. С помощью метода решения регулярной задачи доказываются следующие утверждения:

ТЕОРЕМА 2.1 Справедлива асимптотическая формула собственных чисел задачи на полуоси

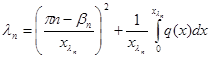, (2.3)

где 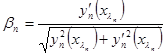[1] .

Справедливость теоремы 2.1 следует из следствия 1.1.

ТЕОРЕМА 2.2 Справедливо неравенство:

. (2.4)

Доказательство теоремы 2.2 можно провести с помощью функций распределения собственных чисел (см. [2]) или с помощью метода, предложенного в первой части работы, и следствия 1.1.

Замечание В случае полуограниченного оператора (), данный выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку собственных чисел.

Следствие 2.1 , где - длина промежутка .

Пример

.

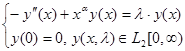Известно, что , где вычисляется явно. Из следствия 2.1 следует:

.

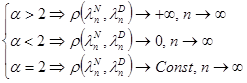III. Сингулярная задача. Случай .

Будем рассматривать задачу

, (2.1)

. (2.2)

Имеет место следующая (см. [3])

ТЕОРЕМА 3.1 Пусть потенциальная функция удовлетворяет следующим условиям

;

, при ;

сохраняет знак для больших ;

, где , при ;

.

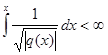Тогда спектр оператора - чисто дискретный и состоит из двух серий собственных чисел, уходящих на и .

Аналогично (как и для полуограниченного оператора) задача на полуоси для расчета собственных чисел заменяется на регулярную задачу, т.е. интервал заменяется на , где - достаточно большое положительное число с дополнительным краевым условием . Нетрудно установить, что погрешность приближенных собственных чисел неполуограниченного оператора (при ) стремится к нулю при . С помощью решения регулярной задачи доказывается следующая